Abstract Algebra II

Rings

• Rings are modeled on the integers

• (`ZZ`, +) is an abelian group

• `ZZ` also has multiplication which satisfies

• `a*(b + c) = a*b + a*c`

• `(b + c)*a = b*a + c*a`

• `a*(b*c) = (a*b)*c`

• Def: A ring is a set `R` with two operations `+`, `*` such that (`R`, `+`) is an abelian group and

• 1) `a*(b*c) = (a*b)*c` (`*` is associative)

• 2) `a*(b + c) = a*b + a*c`, `(b + c)*a = b*a + c*a` for all `a, b, c in R`

• Ex: the set of integer multiples of 3 is a ring, `3ZZ`

• Ex: the real numbers, `RR`

• Ex: the set of real valued functions `f:[a,b]->ZZ`

• Ex: let V be a finite dimensional real vector space. Then `End_RR (V) = {phi: V -> V}` forms a ring

• the multiplication operation is function composition

Properties of Rings

• The second 3 rings (`1in RR`; `f(x) = 1, AA x in [a,b]`; `i``d_v`) have a multiplicative identity

• `a*1 = 1*a = a` (1 is the multiplicative identity)

• But `3a*3b != 3a`

• In `RR` and `{f:[a,b]->RR}`, multiplication is commutative

• `RR` is the only one of these rings with the property that every nonzero element of `RR` has a multiplicative inverse

• `AA a in RR`, `EE b in RR` `s.t. a*b = b*a = 1`

• Rings with a `1` element are said to be unital

• `1` is called a "unity"

• Given a ring `R`, the elements of `R` which have a multiplicative inverse (2-sided) are called the units of `R`

Terminology

• Given a commutative ring `R`, `a, b in R`, we say `a` divides `b` `a`|`b` if `EE c in R` `s.t. a*c = b`

• Since rings are additive groups under addition, given `n in ZZ^+`, we can make sense of `n*a = sum_(i=1)^n a`

• We define `-n*a = -sum_(i=1)^n a` when `n` is positive

• `0*a = 0`

Propositions

• Suppose `a, b, c in R`. Then we have the following properties of multiplication

• `a*0 = 0*a = 0` (`0 in R`, the additive identity)

• `a*(-b) = -a*b`

• `(-a)(-b) = a*b`

• `a*(b-c) = a*b-a*c`

• given any integers `m, n in ZZ`, `(m+n)*a = (m*a) + (n*a)`

• given any integer `m in ZZ`, `m*(a*b) = (m*a)*b = (a)*(m*b)`

• given any integers `m, n in ZZ`, `(m*a)*(n*b) = (m*n)*(a*b)`

• given any integer `n in ZZ`, `n*(a+b) = n*a + n*b`

• given any integer `n in ZZ`, `n*(-a) = -(n*a)`

• If `R` is unital, then

• `(-1)*a = -a` where `-1 in R`

• `(-1)(-1) = 1`

• unity is unique

• if `a` has a left multiplicative inverse and a right multiplicative inverse, then they are equal

• multiplicative inverses are unique

Subrings

• Def: A subring of a ring `R` is a subset `S sube R` which is a ring with the operations of `+` and `*` restricted to `S`

• Unwinding this definition, we see that `+: SxxS->R`, `(s_1, s_2)|->s_1 + s_2` must have image contained in `S` (closed under addition) and `*: SxxS->R`, `(s_1, s_2)|->s_1*s_2` must have image contained in `S` (closed under multiplication)

• We must have `0 in S` and for every `s in S, -s in S` (closed under taking additive inverses)

• In fact, we see that `S` is a subring if and only if `s_1 - s_2 in S` and `s_1*s_2 in S`, `AA s_1, s_2 in S`

• Ex: `3ZZ sube ZZ` is a subring of `ZZ`

• Ex: `QQ sube RR` is a subring of `RR`

• Ex: `{lambda Id}_(lambda in R) sube End_RR(V)` where `V` is a finite dimensional real vector space

Exercises

• Let `R_1, ..., R_n` be rings. The direct sum of `R_1, ..., R_n`, `R_1 o+ R_2 o+ ... o+ R_n` is the set which is the Cartesian product `prod_(i = 1)^n R_i` with ring operations performed component-wise

• `(a_1, ..., a_n) + (b_1, ..., b_n) = (a_1 + b_1, ..., a_n + b_n)`

• `(a_1, ..., a_n) * (b_1, ..., b_n) = (a_1 * b_1, ..., a_n * b_n)`

Exercise: Suppose `R_1, ..., R_n` are rings with nonzero elements. Show that `R = R_1 o+ ... o+ R_n` has unity `<=>` each `R_i` has a unity

(`=>`) Assume `R` has unity, say `(e_1, ..., e_n)`. We want to show that each `R_i` has a unity element. We need to show that `e_i` is the mult. identity of `R_i` for each `i`.

Need to show: given `r_i in R_i`, `e_i*r_i = r_i*e_i = r_i`

Consider a function `f:R_j->R_1 o+ ... o+ R_n, r_j |-> (0, ..., 0, r_j, 0, ..., 0)`

We know that `(0, ..., 0, r_j, 0, ..., 0) * (e_1, ..., e_n) = (0, ..., 0, r_j, 0, ..., 0) = (e_1, ..., e_n)*(0, ..., 0, r_j, 0, ..., 0)`

`=> (0*e_1, ..., r_j*e_j, ..., 0*e_n) = (e_1*0, ..., e_j*r_j, ..., 0*e_n)`

`=> (0, ..., 0, r_j*e_j, 0, ..., 0) = (0, ..., 0, e_j*r_j, 0, ..., 0)`

This shows that `e_j*r_j = r_j = r_j*e_j, AA r in R_j => e_j` is a mult identity of `R_j`

(`lArr`) Assume that each `R_i` has a mult. identity. We need to show that `R` does too.

Say `e_i` is the mult. identity of `R_i`. We claim that `(e_1, ..., e_n)` is the mult. identity of `R`. We must show that `(e_1, ..., e_n)*(r_1, ..., r_n) = (r_1, ..., r_n)*(e_1, ..., e_n) = (r_1, ..., r_n), AA (r_1, ..., r_n) in R`

`(e_1, ..., e_n)*(r_1, ..., r_n) = (e_1*r_1, ..., e_n*r_n) = (r_1, ..., r_n)`

`(r_1, ..., r_n)*(e_1, ..., e_n) = (r_1*e_1, ..., r_n*e_n) = (r_1, ..., r_n)`

Exercise: Suppose that there is a positive even integer `n` `s.t. a^n = a` for all `a in R`. Show that `-a = a` for all `a in R`.

We can write `n = 2k` for some positive integer `k`

`-a = (-a)^n = (-a)^(2k) = ((-a)^2)^k = (a^2)^k = a^(2k) = a^n = a`

Exercise: Suppose that there is an integer `n > 1` such that `x^n = x, AA x in R`. If `m` is a positive integer such that `a^m = 0` for some `a`, show that `a = 0`

Case 1: `m <= n`

`a = a^n = a^m * a^(n-m) = 0 * a^(n-m) = 0`

Case 2: `m > n`

Choose `m` to be the smallest positive integer `s.t. a^m = 0`

Suppose for a contradiction `m > n`

`0 = a^m = a^n * a^(m-n) = a*a^(m-n) = a^(m-n+1)`

Since m was chosen to be the smallest positive integer with this property, `m-n+1 >= m => -n + 1 >= 0 => 1 >= n`

This contradicts the assumption that `n > 1`

Integral Domains

• `ZZ` has more structure than an arbitrary ring does

• `ZZ` is a commutative ring

• `ZZ` has a mult. identity

• `ZZ` has the property that if `a, b != 0`, then `ab != 0`

• Def: A zero-divisor in a commutative ring is a nonzero element `z in R` `s.t.` there exists a nonzero element `y in R` `s.t.` `zy = 0`

• Def: An integral domain is a unital commutative ring `R` `s.t.` if `a, b in R` `s.t. ab = 0`, then either `a = 0` or `b = 0`

• We almost have division in integral domains: we have cancellation

Proposition: Let `R` be a domain. Suppose that `a != 0 in R`. Then `ab = ac => b= c`

`ab = ac => ab - ac = 0 => a(b-c) = 0`

Since `a != 0`, `b-c = 0 => b = c`

• Ex: `QQ` is a domain

• Ex: the Gaussian integers `ZZ[i] = {a + bi | a, b in ZZ}` is a domain

• Ex: `CC[x]` - the ring of polynomials in a single indeterminate `x` with coefficients `in CC` is a domain

• NonEx: `ZZ // (4ZZ)` is not a domain because `[2]_4 * [2]_4 = [4]_4 = [0]_4`

• Def: A field is a domain `F` `s.t.` every nonzero element of `F` has a mult. inverse

• Ex: `RR` is a field

• Ex: `CC(t) = {f(t)/g(t) | f(t), g(t) in CC(t)}` the ring of rational functions whose coefficients are in `CC` is a field

Proposition: Let `D` be a finite integral domain. Then `D` is a field.

Need to show that every nonzero element has a mult. inverse

Let `a != 0 in D`. Consider the function `phi_a: D->D`, `y |-> ay`

If we show that `phi_a` is surjective, then we are done

Since `D` is finite, by the pigeonhole principle, `phi_a` is surjective `<=> phi_a` is injective

Therefore, it suffices to show that `phi_a` is injective

Suppose `b, c in D` `s.t.` `phi_a(b) = phi_a(c) => ab = ac`

Since `a != 0` and `D` is a domain, we conclude that `b = c => phi_a` is injective

Since `phi_a` is surjective, if we fix `1 in D`, we can find an element `b in D` `s.t.` `phi_a(b) = ab = 1 => b` is the mult. inverse of `a`

Corollary: `ZZ // pZZ` is a field `<=> p` is prime

(`=>`) Suppose `ZZ // pZZ` is a field but `p` is not prime

Then `p = qr`, `1 < q, r < p`

Then `[q]_p*[r]_p = [p]_p = [0]_p => ZZ // pZZ` has zero-divisors, which contradicts `ZZ // pZZ` is a field

(`lArr`) If `p` is prime, then we must show `ZZ // pZZ` is a domain by the previous result

Suppose `[a]_p * [b]_p = [0]_p <=> ab = pk` for some integer `k`

`p` prime `=> p|ab <=> p|a` or `p|b <=> [a]_p = [0]_p` or `[b]_p = [0]_p => ZZ // pZZ` is a domain

Proposition: If `R` is an integral domain and `S` is a subring of `R` which contains `1 in R`, then `S` itself is an integral domain

`S` is commutative ✓

`S` has a mult. identity ✓

If `s_1, s_2 in S` `s.t.` `s_1*s_2 = 0 in S`, this same equation holds in `R`

Since `R` is a domain, `s_1s_2 = 0 => s_1 = 0 or s_2 = 0`

• Ex: Notice that in `ZZ // nZZ`, `n[a]_n = [na]_n = [0]_n`

• Multiplication by `n` kills all elements of `ZZ // nZZ`

• Ex: Consider `CC` (along with all subrings `R` of `CC` containing `1`). There does not exist a positive integer `n` `s.t.` `n*z = 0` `AA z in CC` and `n*z = 0` `AA z in R`

• The only integer which kills all of `CC` (or `R`) is `0`

• The integer `n` in these examples is called the characteristic of the ring

• Def: the characteristic of a ring `R` is the least nonnegative integer `n` `s.t.` `n*r = 0` `AA r in R`

• `char(ZZ // nZZ) = n`, `char(CC) = 0`

• When `R` is a unital commutative ring, we can relate `char(R)` to the order of `1 in R` (as an abelian group under `+`)

• If `1` has infinite order in `R`, then `char(R) = 0`

• If `1` has finite order, say `n`, then `char(R) = n`

• Since `o``rd(1) = n, n*1 = 0`

• `n*r = (n*1)r = 0` `AA r in R`

• `=> n` kills everything in `R`

• Therefore, `n >= char(R)`

• We know that `char(R)*1 = 0 => n|char(R) => n <= char(R)`

• So `n = char(R)`

Proposition: If `R` is an integral domain, then `char(R) = 0` or `char(R) = p` for some prime number `p`

Suppose that `R` is an integral domain and `char(R) != 0`. Suppose for a contradiction `char(R)` is not prime.

If `char(R)` is not prime, `EE n, q in ZZ^+` `s.t.` `p = nq`, `1 < n, q < p`

Notice that `(n*1)*(q*1) = (nq)*1 = p*1 = 0` where `(n*1)` and `(q*1)` are not equal to `0`

This contradicts the fact that `R` is a domain

• If `char(R) = n`, then the subring generated by `1` in `R` is isomorphic to `ZZ // nZZ`

Exercise: Suppose `R` is a commutative ring without zero divisors. (`R` is not necessarily unital.) Show that `char(R)` is `0` or prime.

Suppose `R` is commutative with no zero divisors. Let `p = char(R)` and suppose `p != 0`. Suppose for a contradiction that `p` is not prime.

`=> EE n, q in ZZ^+` `s.t.` `p = nq`, `1 < n, q < p`

Claim: we can find `a, b in R` `s.t.` `n*a != 0` and `q*b != 0`

Suppose not. Then for all `r in R`, `n*r = 0` and `q*r = 0`

But `1 < n, q < p = char(R)`

This contradicts the fact that `p` is the least nonnegative integer `s.t.` `p*r = 0` `AA r in R`

Thus, we can find `a, b in R` `s.t.` `n*a != 0` and `q*b != 0`

`(n*a) * (q*b) = (n*q)*(a*b) = p*(a*b) = 0`

This contradicts the assumption that `R` does not have zero divisors

Suppose `R` is a commutative ring with prime characteristic `p`. Show that `(x + y)^p = x^p + y^p, AA x, y in R` and `(x + y)^(p^n) = x^(p^n) + y^(p^n)`, for all positive integers `n`

`(x + y)^p = sum_(i = 0)^p ((p), (i)) x^iy^(p-i)`

`= ((p), (0))x^0y^(p) + ((p), (1))xy^(p-1) + ... + ((p), (p-1))x^(p-1)y + ((0), (p))x^p`

`= y^p + pxy^(p-1) + ((p), (2))x^2y^(p-2) + ... + ((p), (p-2))x^(p-2)y^2 + px^(p-1)y + x^p`

It suffices to show that `((p), (i))` is divisible by `p`

`((p), (i)) = (p!) / ((p-i)!p!) = (p * ... * (p-i+1) * (p-i) * ... * 1) / ((p-i)*...*1*i!)`

` = (p*...*(p-i+1)) / (i!) = p(((p-1)*...*(p-i+1)) / (i!))`

`=> p` divides `((p), (i))`

So `y^p + p(_) + ... + p(_) + x^p = y^p + x^p`

Base Case: We just proved `(x+y)^(p^1) = x^(p^1) + y^(p^1)` for all `x, y in R`

Inductive Hypothesis: Assume that for some integer `k >= 1`, `(x+y)^(p^k) = x^(p^k) + y^(p^k)`

`(x+y)^(p^(k+1)) = ((x+y)^(p^k))^p = (x^(p^k) + y^(p^k))^p = ((x^(p^k))^p + (y^(p^k))^p)`

`= x^(p^(k+1)) + y^(p^(k+1))`

By induction, `(x+y)^(p^n) = x^(p^n) + y^(p^n), AA n in ZZ^+`

Exercise: Let `R` be a finite commutative ring with unity. Prove that every nonzero element of `R` is either a zero-divisor or a unit

Let `a != 0` be a non zero-divisor. We claim that `a` is a unit

Define `phi_a: R -> R`, `x |-> ax`. We claim that `phi_a` is injective

Suppose `x, y in R` `s.t.` `phi_a (x) = phi_a (y)`

Then `ax = ay <=> a(x-y) = 0`

Since `a` is not a zero divisor and `a != 0`, `x-y = 0 <=> x = y`

By the Pigeonhole Principle, `phi_a` is also surjective

If we fix `1 in R`, we can find `b in R` `s.t.` `phi_a (b) = 1 <=> ab = 1 => a` is a unit

• Let `R` be an integral domain. A subdomain `S` of `R` is a subring of `R` `s.t.` `S` contains the `1` element of `R`.

Exercise: Let `P = {n*1 | n in ZZ} sube R`. Show that `P` is contained in every subdomain. What is the order of `P`?

Let `S` be a subdomain of `R`. We claim that `P sube S`

Any element of `P` has the form `n*1` for some integer `n`

Case 1 `(n = 0)`: `0*1 = 0 in S`

Case 2 `(n > 0)`: `n*1 = sum_(i = 1)^n 1 in S` because `S` is closed under addition

Case 3 `(n < 0)`: `n = -n', n' > 0`. `n'*1 in S => -n'*1 in S` so `S` is closed under taking additive inverses

Therefore `P sube S`

Claim: the order of `P = char(R)`

If `n*1 = 0 in R, n*1 = 0 in P`

`n = char(R), o rd(P) | char(R) => o rd(P) <= char(R)`

`o rd(P)*1 = 0 in P => o rd(P)*1 = 0 in R => char(R) <= o rd(P)`

• A ring element `a` is idempotent if `a^2 = a`

Exercise: Prove that the only idempotent elements of an integral domain are `0` and `1`

If `a` is idempotent, then `a^2 = a <=> a^2 - a = 0 <=> a(a-1) = 0`

`<=> a = 1` or `a = 0`

Ideals

• From group theory, the cosets of a normal subgroup `N` in a group `G` form a group themselves

• It turns out that, with rings, the quotient of a ring by an arbitrary subring need not be a ring itself

• Definition: A (two-sided) ideal of a ring `R` is a subring `I sube R` `s.t.` `rI sube I, Ir sube I` `AA r in R`

• Definition: An ideal of a commutative ring `R` is a subset `I sube R` `s.t.` `I` is a subgroup of the additive group of `R` and `rI sube I` for all `r in R`

• Ex: Fix a ring `R`. The set consisting of `{0}` is an ideal generated by a single element

• Ex: `I = {f in CC[t]` `|` `t|f} = (t) = {tf}`

• Let `f, g in I => EE f', g' in CC[t]` `s.t.` `f = f't, g = g't`

• `f + g = f't + g't = t(f' + g')`

• Let `h in CC[t], f in I => EE f' in CC[t]` `s.t.` `f = f't`

• Then `hf = h*f't = t(hf') in I`

• This is an example of a principal ideal: an ideal generated by a single element

• Ex: Given a ring `R` and elements `a_1, ..., a_n in R`, we can consider the set of all `R`-linear combinations of `a_1, ..., a_n`

• `{r_1a_1 + ... + r_na_n | r_i in R} = (a_1, ..., a_n)` is the ideal generated by `a_1, ..., a_n`

• Let `sum_(i = 1)^n r_ia_i, sum_(i = 1)^n s_ia_i in (a_1, ..., a_n)`

• We claim that `sum_(i = 1)^n r_ia_i - sum_(i= = 1)^n s_ia_i in (a_1, ..., a_n)`

• `sum_(i = 1)^n r_ia_i - sum_(i= = 1)^n s_ia_i = sum_(i = 1)^n (r_i-s_i)a_i in (a_1, ..., a_n)`

• Let `r in R, sum_(i = 1)^n r_ia_i in (a_1, ..., a_n)`

• We claim that `r*sum_(i = 1)^n r_ia_i in (a_1, ..., a_n)`

• `r*sum_(i = 1)^n r_ia_i = sum_(i = 1)^n rr_ia_i in (a_1, ..., a_n)`

Exercise: Given two ideals `I, J in R`, let `I+J = {i + j | i in I, j in J}`. Show that `I+J` is an ideal

Let `i_1 + j_1 in I + J` and `i_2 + j_2 in I + J` for `i_1, i_2 in I` and `j_1, j_2 in J`

`(i_1 + j_1) - (i_2 + j_2) = (i_1 - i_2) + (j_1 - j_2) in I + J`

Let `i + j in I + J`. Let `r in R`.

`r(i + j) = ri + rj in I + J` and `(i + j)r = ir + ij in I + J`

Exercise: Let `I, J` be ideals of a ring `R`. Let `IJ = {sum_(k = 1)^n i_kj_k | i_k in I, j_k in J, n in ZZ^+}`. Show that `IJ` is an ideal

Let `sum_(k = 1)^n i_kj_k, sum_(l = 1)^m i'_lj'_l in IJ`

Then `sum_(k = 1)^n i_kj_k - sum_(l = 1)^m i'_lj'_l = sum_(k = 1)^n i_kj_k + sum_(l = 1)^m (-i'_l)(j'_l) in IJ`

Let `r in R`. Let `sum_(k = 1)^n i_kj_k in IJ`

`r*sum_(k = 1)^n i_kj_k = sum_(k = 1)^n ri_kj_k = sum_(k = 1)^n (ri_k)j_k in IJ`

`(sum_(k = 1)^n i_kj_k)*r = ... = sum_(k = 1)^n i_k(j_kr) in IJ`

Exercise: Let `I, J` be two ideals of `R`. Show that `I nn J` is an ideal

From group theory, since `I, J` are subgroups of `(R, +)`, `I nn J` is a subgroup of `(R, +)`

Let `z in I nn J`. Let `r in R`. We claim that `rz, zr in I nn J`

`z in I nn J => z in I => rz in I`

`z in I nn J => z in J => rz in J`

`=> rz in I nn J` (similarly for `zr`)

Exercise: If `I` and `J` are two ideals in a unital commutative ring, show that `IJ sube I nn J`

Let `i in I, j in J`

`ij = (i)j in J` (`i in R, j in J`)

`ij = i(j) in I` (`i in I, j in R`)

`=> ij in I nn J`

If `I` and `J` are two ideals in a unital commutative ring `R` `s.t.` `I + J = R`, show that `IJ = I nn J`

Since `I + J = R`, given any `r in R`, we can write `r = i + j` for some `i in I, j in J`

In particular, `1 = i + j` for some `i in I, j in J`

Let `z in I nn J`. We claim `z in IJ`

`z = 1*z = (i + j)*z = iz + jz`

`z in I nn J => z in I, z in J`

Since `i in I, z in J, iz in IJ`

Since `j in J, z in I, jz in IJ`

So `iz + jz in IJ`

Quotient Rings

• Let `R` be a ring and let `I` be an ideal

• Let `R//I = {r + I | r in R}`. We will put a ring structure on `R//I`

• From group theory, `R` is an abelian group under `+` and `I` is a subgroup

• Therefore, `R//I` is a group under `+`, which is defined as `(r_1 + I) + (r_2 + I) = (r_1 + r_2 + I)`

• We define multiplication by `(r_1 + I) * (r_2 + I) = (r_1r_2 + I)`

We claim that this is well-defined

Suppose `r_1 + I = s_1 + I, r_2 + I = s_2 + I`

We need to show that `r_1r_2 + I = s_1s_2 + I`

`r_1 + I = s_1 + I <=> r_1 - s_1 in I`

`r_2 + I = s_2 + I <=> r_2 - s_2 in I`

Notice that `r_1r_2 + I = s_1s_2 + I <=> r_1r_2 - s_1s_2 in I`

Since `r_1-s_1, r_2-s_2 in I`, we see that `(r_1-s_1)(r_2-s_2) = r_1r_2 - s_1r_2 - r_1s_2 + s_1s_2`

`= r_1r_2 - r_2s_1 - r_1s_2 + s_1s_2`

`= r_1r_2 - r_2s_1 - r_1s_2 + s_1s_2 + (s_1s_2 - s_1s_2)`

`= (r_1r_2 - s_1s_2) - s_1(r_2-s_2) - s_2(r_1-s_1)`

`=> r_1r_2 - s_1s_2 in I`

• Ex: `ZZ // nZZ` is the quotient of `ZZ` by the ideal `nZZ`

• Ex: Let's determine what the cosets of `(t)` in `CC[t]` are. What is `(CC[t])/((t))`?

• Given `f(t) in CC[t]`, we can consider the polynomial `f(t) - f(0)` which lies in `(t)`

• Therefore, `f(t) + (t) = f(0) + t` as cosets

Ex: Classify all ideals in `ZZ`. We claim that every ideal has the form `nZZ` for some `n in ZZ^+`

Let `I != (0)` be an ideal of `ZZ`. Let `n` be the least positive integer in `I`

We claim `I = nZZ`. It suffices to show that `n | m`, `AA m in I`

Let `m != 0 in I`. Assume that `m > 0`. Consider `gcd(m,n)`

By the Euclidean algorithm, we can write `gcd(m,n) = am + bn` for some `a, b in ZZ^+`

`m, n in I => gcd(m,n) = am + bn in I`

Therefore, `gcd(m,n) in I` but `0 < gcd(m,n) <= n => gcd(m,n) = n` (since `n` is the least positive integer in `I`) `=> n|m`

If `m < 0`, then `-m in I` and the argument we just proved shows that `n|-m =>n|m`

`pZZ` where `p` is prime is a "special type" of ideal

Let `a, b in ZZ` `s.t.` `p|ab`. Then `p|a` or `p|b`

`ab in pZZ <=> p|ab => p|a` or `p|b <=> a in pZZ` or `b in pZZ`

So `ab in pZZ => a in pZZ` or `b in pZZ`

• If `aZZ, bZZ` are two ideals of `ZZ`, then `aZZ * bZZ sube pZZ => aZZ sube pZZ` or `bZZ sube pZZ`

• Such ideals with this property are called prime ideals

• Definition: An ideal `p sube R` is a prime ideal if `p` is a proper ideal and whenever `ab in p`, we must have `a in p` or `b in p` `AA a, b in R`

`pZZ` is a prime ideal `<=> p` is prime

(`lArr`) We've already seen that if `p` is prime, then `pZZ` is a prime ideal

(`=>`) Suppose `pZZ` is a prime ideal. It suffices to show that if `p = ab` where `a, b > 0`, then `p = a` or `p = b`

If `p = ab`, then `ab in pZZ`

Since `pZZ` is a prime ideal, we must have either `a in pZZ` or `b in pZZ`

`a in pZZ <=> p|a` and `b in pZZ <=> p|b`

Either `p|a` or `p|b`

Since `a, b, p > 0`, `p|a` and `a|p` `=> a = p`

`p|b` and `b|p` `=> b = p`

`=> p` is a prime number

• Definition: An ideal `m` of a commutative ring `R` is said to be maximal if `m sub R` (`m` is a proper ideal) and, whenever `I` is an ideal `s.t.` `m sube I`, we must have `I = m` or `I = R`

• Ex: Returning to `ZZ`, it turns out that `pZZ` is not only prime, but also maximal when `p` is prime

We claim `pZZ` is maximal

Suppose `pZZ sube I` where `I` is an ideal of `ZZ`

We've already seen that `I = nZZ` for some positive integer `n`

Therefore, `pZZ sube nZZ`

In particular, `p in pZZ sube nZZ => p in nZZ <=> n|p`

Since `p` is prime, we either have `n = p` (`=> nZZ = pZZ`) or `n = 1` (`=> nZZ = ZZ`)

So `pZZ` is maximal

Proposition: If `R` is a commutative ring with unity, then the following are equivalent

1) `p` is a prime ideal

2) `R // p` is an integral domain

and

3) `M` is a maximal ideal

4) `R // M` is a field

(`1 => 2`): Suppose `p` is a prime ideal. We already know that `R // p` is a commutative ring with unity. We must show that `R // p` has no zero-divisors

Suppose `(x + p)(y + p) = (0 + p) => (xy + p) = (0 + p) <=> xy in p`

Since `p` is a prime ideal, `xy in p <=> x in p` or `y in p`

If `x in p`, then `x + p = 0 + p`

If `y in p`, then `y + p = 0 + p`

Then `R // p` is an integral domain

(`2 => 1`): Suppose `R // p` is an integral domain. Let `x, y in R` `s.t.` `xy in p`

We claim that `x in p` or `y in p`

Consider `(x + p)*(y + p) = (xy + p)`

Since `xy in p, (xy + p) = (0 + p)`

Since `R // p` is an integral domain, we must have either `x + p = 0 + p <=> x in p` or `y + p = 0 + p <=> y in p`

Therefore `p` is prime

(`3 => 4`): Assume that `M` is a maximal ideal

Let `x + M != 0 + M in R // M`

We claim that there exists `y + M in R // M` `s.t.` `(x + M)*(y + M) = 1 + M => xy + M = 1 + M`

We need to show that we can find `y in R` `s.t.` `xy = 1 (mod M)`

Consider the ideal `(x) + M sube R`

We know that `(x) + M != M` since `x notin M`

Since `(x) + M sup M` and `M` is maximal, `(x) + M = R`

We need to use the fact that `(x) + M = R` to produce an element `y` `s.t.` `xy - 1 in M`

Since `(x) + M = R`, we can find `y in R, m in M` `s.t.` `xy + m = 1 => xy - 1 = m in M`

So `xy = 1 (mod M) <=> y + M` is the multiplicative inverse of `x + M`

(`4 => 3`): Suppose `R // M` is a field

Let `I` be an ideal of `R` `s.t.` `M sube I`

We must show that `I = R <=> 1 in I`

Consider `(I + M) // M = {i + M | i in I}`

It turns out that `(I + M) // M` is an ideal of `R // M`

Let `i_1 + M, i_2 + M in (I + M) // M`

Notice that `(i_1 + M) - (i_2 + M) = ((i_1 - i_2) + M) in (I + M) // M`

Therefore, `(I + M) // M` is a subgroup of `R // M`

Let `i + M in (I + M) // M, r + M in R // M`

Notice that `(r + M)*(i + M) = (ri + M) in (I + M) // M`

Therefore, `(I + M) // M = {i + M | i in I}` is an ideal of `R // M`

This is not the zero ideal since `I sup M`

Therefore, there exists `i + M != 0 + M in (I + M) // M`

`R // M` is a field `=> EE j + M in R // M` `s.t.` `(i + M)(j + M) = 1 + M = ij + M`

Since `(I + M) // M` is an ideal containing `i + M`, `(i + M)(j + M) = 1 + M in (I + M) // M`

Since `(ij + M) = (1 + M), 1 - ij in M`

Remember `i in I => ij in 1` and `m sub I => 1 - ij in I`

Therefore, `1 - ij = i' in I`, so `1 = ij + i' in I => 1 in I => I = R`

Ring Homomorphisms

• In group theory, we saw that group homomorphisms allow us to translate data from one group to another

• `phi(g_1 **_1 g_2) = phi(g_1) **_2 phi(g_2)`

• Definition: Let `R, S` be rings. A ring homomorphism `phi: R -> S` is a function from `R` to `S` `s.t.` `AA r_1, r_2 in R`

• 1) `phi(r_1 + r_2) = phi(r_1) + phi(r_2)`

• 2) `phi(r_1r_2) = phi(r_1)phi(r_2)`

• Definition: Suppose `R, S` have unity elements. A ring homomorphism is unital if `phi(1_R) = 1_S`

• Definition: A ring isomorphism is a ring homomorphism which is both one-to-one and onto

Ex: Let `n` be a positive integer. Then reduction modulo `n` is a ring homomorphism: `pi_n: ZZ -> ZZ // nZZ, a |-> [a]_n`

Let `a, b in ZZ`

Then `pi_n(a + b) = [a + b]_n = [a]_n + [b]_n = pi_n(a) + pi_n(b)`

Also `pi_n(ab) = [ab]_n = [a]_n[b]_n = pi_n(a)pi_n(b)`

Since `pi_n(1) = [1]_n, pi_n` is also unital

• This is a special case of the natural projection homomorphism:

• Given a ring `R` and a two-sided ideal `I`, `pi_I: R -> R // I, r |-> r + I`

Ex: Let `z in CC`. Consider the map `ev_z: CC[t] -> CC, f |-> f(z)`. This is a ring homomorphism

Let `f, g in CC[t]`.

Then `ev_z(f+g) = (f+g)(z) = f(z) + g(z) = ev_z(f) + ev_z(g)`

`ev_z(fg) = (fg)(z) = f(z)g(z) = ev_z(f)ev_z(g)`

• Definition: Let `phi: R -> S` be a homomorphism of rings. Define the kernel of `phi` to be `ker(phi) = {r in R | phi(r) = 0}`

Find the kernel of `ev_0: CC[t] -> CC, f |-> f(0)`

We claim that `ker(ev_0) = (t)`

Let `f in ker(ev_0) => ev_0(f) = 0 <=> f(0) = 0 => f` has no constant term, so `t|f <=> f in (t)`

Let `f in (t)`. Then there exists `f' in CC[t]` `s.t.` `f = tf'`

Notice that `ev_0(f) = ev_0(tf') = 0*f'(0) = 0 => tf' = f in ker(ev_0)`

Propositions: Let `R, S` be rings. Let `phi: R -> S` be a ring homomorphism. Let `A sube R` be a subring and let `B sube S` be an ideal

`phi(0) = 0`

`phi(r^n) = (phi(r))^n` `AA r in R, n in ZZ^+`

`phi(nr) = n*phi(r)` `AA r in R, n in ZZ^+`

If `phi` is onto, then if `A` is an ideal, then `phi(A)` is an ideal

The preimage of `B`, `phi^-1(B) = {r in R | phi(r) in B}` is an ideal

If `R` is commutative, so is `phi(R)`

If `R` is unital, `S` is not the zero ring, and `phi` is onto, then `S` is unital and `phi(1)` is the unity of `S`

`phi` is one-to-one `<=> ker(phi) = 0`

If `phi` is an isomorphism from `R` to `S`, then `phi^-1` is an isomorphism from `S` to `R`

WTS `phi(0) = 0`

`0 + 0 = 0 => phi(0 + 0) = phi(0)`

Since `phi` is a ring homomorphism, `phi(0 + 0) = phi(0) + phi(0)`

`=> phi(0) + phi(0) = phi(0) => phi(0) = 0`

WTS If `phi` is onto, then if `A` is an ideal, then `phi(A)` is an ideal

Suppose `A` is an ideal and `phi` is onto

Let `s_1, s_2 in phi(A) sube S`

Then we can find `a_1, a_2 in A` `s.t.` `phi(a_1) = s_1, phi(a_2) = s_2`

Notice that `s_1 - s_2 = phi(a_1) - phi(a_2) = phi(a_1 - a_2)`

Since `A` is an ideal, `a_1 - a_2 in A => s_1 - s_2 = phi(a_1 - a_2) in phi(A)`

Let `s in phi(A)`. Let `s' in S`. We claim `s's in phi(A)`

Since `s in phi(A), EE a in A` `s.t.` `phi(a) = s`

Since `phi` is onto, `EE r in R` `s.t.` `phi(r) = s'`

Notice that `s's = phi(r)*phi(a) = phi(r*a)`

`A` is an ideal and `a in A => ra in A => s's = phi(ra) in phi(A)`

WTS The preimage of `B`, `phi^-1(B) = {r in R | phi(r) in B}` is an ideal

Let `r_1, r_2 in phi^-1(B)`. We need to show that `r_1 - r_2 in phi^-1(B)`

`r_1, r_2 in phi^-1(B) => phi(r_1), phi(r_2) in B`

Notice that `phi(r_1) - phi(r_2) in B` since `B` is an ideal

But `phi(r_1) - phi(r_2) = phi(r_1 - r_2) in B <=> r_1 - r_2 in phi^-1(B)`

Let `r in phi^-1(B), r' in R`. We claim `r'r in phi^-1(B)`

Notice that `phi(r'r) = phi(r')*phi(r) in B` since `B` is an ideal and `phi(r) in B`

`phi(r'r) in B <=> r'r in phi^-1(B)`

WTS If `R` is unital, `S` is not the zero ring, and `phi` is onto, then `S` is unital and `phi(1)` is the unity of `S`

Suppose `phi: R -> S` is onto, `1 in R`

We claim that `phi(1)` is a unity of `S <=>` given any `s in S, phi(1)*s = s = s*phi(1)`

Let `s in S`. Since `phi` is onto, we can find `r in R` `s.t.` `phi(r) = s`

Then `phi(1)*s = phi(1)*phi(r) = phi(1*r) = phi(r) = s`

WTS `phi` is one-to-one `<=> ker(phi) = 0`

`(=>)` Suppose `phi` is one-to-one. Since `0` is an element of `R` which maps to `0 in S`, `phi` is one-to-one `=>` if `phi(r) = 0`, then `r = 0`

`(lArr)` Suppose `ker(phi) = 0`. Let `r_1, r_2 in R` `s.t.` `phi(r_1) = phi(r_2)`

Then `phi(r_1) - phi(r_2) = 0 => phi(r_1 - r_2) = 0 => r_1 - r_2 in ker(phi)` so `r_1 - r_2 = 0 <=> r_1 = r_2`

WTS If `phi` is an isomorphism from `R` to `S`, then `phi^-1` is an isomorphism from `S` to `R`

Suppose `phi` is an isomorphism. Then `phi` is a one-to-one and onto homomorphism

Since `phi` is one-to-one and onto, `EE phi^-1: S -> R` `s.t.` `phi @ phi^-1 =` `i``d_s`, `phi^-1 @ phi =` `i``d_r`

We claim that `phi^-1(s_1 + s_2) = phi^-1(s_1) + phi^-1(s_2)` and `phi^-1(s_1s_2) = phi^-1(s_1)phi^-1(s_2) AA s_1, s_2 in S`

Let `s_1, s_2 in S`. Then we can find `r_1, r_2 in R` `s.t.` `phi(r_1) = s_1, phi(r_2) = s_2`

`phi^-1(s_1 + s_2) = phi^-1(phi(r_1) + phi(r_2)) = phi^-1(phi(r_1 + r_2))`

`= r_1 + r_2 = phi^-1(s_1) + phi^-1(s_2)`

`phi^-1(s_1s_2) = phi^-1(phi(r_1)phi(r_2)) = phi^-1(phi(r_1r_2))`

`= r_1r_2 = phi^-1(s_1)phi^-1(s_2)`

Exercise: Show that if `phi: R -> S` is a ring homomorphism, then `ker(phi)` is an ideal of `R`

Let `r_1, r_2 in ker(phi)`. We claim `r_1 - r_2 in ker(phi)`

`phi(r_1 - r_2) = phi(r_1) - phi(r_2) = 0 - 0 = 0 => r_1 - r_2 in ker(phi)`

Let `r' in R, r in ker(phi)`. We claim that `r'r in ker(phi)`

`phi(r'r) = phi(r')phi(r) = phi(r')*0 = 0 => r'r in ker(phi)`

Exercise: Show that if `I` is a two-sided ideal of `R`, then `I` is the kernel of some ring homomorphism

Consider `pi_I: R -> R // I`. We claim that `ker(pi_I) = I`

`(supe)` If `i in I => pi_I(i) = i + I = 0 + I` since `i in I`

`(sube)` Suppose `r in ker(pi_I) => pi_I(r) = 0 + I`

`pi_I(r) = r + I = 0 + I <=> r in I`

Ideal Correspondence Theorem: Let `R` be a commutative ring with unity and let `I` be an ideal. Then there is a one-to-one order-preserving correspondence between ideals of `R` which contain `I` and ideals of `R // I`



Since `pi_I` is surjective, given any ideal `J sube R` which contains `I`, `pi_I(J)` is an ideal of `R // I`

`pi_I(J) = {j + I | j in J} = (J + I) // I`

We claim that `pi_I^-1(pi_I(J)) = J`

`(supe)` If `j in J`, then `pi_I(j) = j + I in pi_I(J) => j in pi_I^-1(pi_I(j))`

`(sube)` Suppose `r in pi_I^-1(pi_I(J)) => pi_I(r) in pi_I(J) => r + I in pi_I(J)`

`EE j in J` `s.t.` `r + I = j + I <=> r - j in I`

Since `I sube J, r - j in J => r in J`

Let `H sube R // I`. Consider `pi_I^-1(H) sube R`. We claim that `pi_I^-1(H) supe I`

Let `i in I => pi_I(i) = i + I = 0 + I`

Since `H` is an ideal, `0 + I in H => i in pi_I^-1(H) => I in pi_I^-1(H)`

We claim that `pi_I(pi_I^-1(H)) = H`

Since `pi_I` is surjective, this is true.

Therefore, `pi_I: {I sube J sube R} -> {(0 + I) // I sube H sube R // I}` is a bijection

Suppose `I sube J_1 sube J_2`. We claim that `pi_I(J_1) sub pi_I(J_2)`

We always have `J_1 sube J_2 => pi_I(J_1) sube pi_I(J_2)`

If `pi_I(J_1) = pi_I(J_2) => J_1 = J_2` since correspondence is one-to-one

So we must have `pi_I(J_1) sub pi_I(J_2)`

Suppose `H_1 sub H_2 sube R // I`. We claim that `pi_I^-1(H_1) sub pi_I^-1(H_2)`

We always have `pi_I^-1(H_1) sube pi_I^-1(H_2)`

If `pi_I^-1(H_1) = pi_I^-1(H_2)`, then since `pi_I^-1` is a bijection, we must have `H_1 = H_2`

Therefore, `pi_I^-1(H_1) sub pi_I^-1(H_2)`

• Through this order-preserving correspondence, we can think of the set of ideals of `R // I` as a subset of the set of ideals of `R`

• In particular, the set of prime ideals of `R // I` can be viewed as a subset of the set of prime ideals of `R`

First Isomorphism Theorem: If `phi: R -> S` is a ring homomorphism, then there is an isomorphism of rings `bar phi: R // ker(phi) -> phi(R), r + ker(phi) |-> phi(r)`

We need to prove that `bar phi` is well-defined.

Let `r_1 + ker(phi) = r_2 + ker(phi) in R // ker(phi)`

We claim `bar phi(r_1 + ker(phi)) = bar phi(r_2 + ker(phi))`

`bar phi(r_1 + ker(phi)) = phi(r_1) and bar phi(r_2 + ker(phi)) = phi(r_2)`

Therefore, we must show that if `r_1 + ker(phi) = r_2 + ker(phi)`, then `phi(r_1) = phi(r_2)`

Suppose `r_1 + ker(phi) = r_2 + ker(phi) <=> r_1 - r_2 in ker(phi)`

`=> phi(r_1 - r_2) = 0 => phi(r_1) - phi(r_2) = 0 => phi(r_1) = phi(r_2)`

Next we check that `bar phi` is a ring homomorphism

Let `r_1 + ker(phi), r_2 + ker(phi) in R // ker(phi)`

Consider `bar phi((r_1 + ker(phi)) + (r_2 + ker(phi)))`

`= bar phi(r_1 + r_2 + ker(phi)) = phi(r_1 + r_2) = phi(r_1) + phi(r_2)`

`= bar phi(r_1 + ker(phi)) + bar phi(r_2 + ker(phi))`

`bar phi((r_1 + ker(phi)) * (r_2 + ker(phi))) = bar phi(r_1r_2 + ker(phi)) = phi(r_1r_2)`

`= phi(r_1)phi(r_2) = bar phi(r_1 + ker(phi)) bar phi(r_2 + ker(phi))`

We must check that `bar phi` is onto. Fix `s in phi(R)`

Then we can find `r in R` `s.t.` `phi(r) = s`

Notice that `bar phi(r + ker(phi)) = phi(r)`, so `bar phi` is onto

Suppose that `r + ker(phi) in ker(bar phi) => bar phi(r + ker(phi)) = 0`

But `bar phi(r + ker(phi)) = phi(r) = 0 <=> r in ker(phi) => r + ker(phi) = 0 + ker(phi)`

So `bar phi` is injective

• Last time we defined `ev_0: CC[t] -> CC, f |-> f(c)`

• We saw that this is a ring homomorphism which maps onto `CC`

• We saw that `ker(ev_0) = (t)`

• Therefore, by the First Isomorphism Theorem, `CC[t] // (t) ~= CC`

• Suppose `I` is an ideal of a commutative ring `R`. Then we can use the First Isomorphism Theorem to determine what `R // I` is isomorphic to

• Suppose we have a hunch that `R // I ~= S`. To prove this, we can exhibit a surjective ring homomorphism `phi: R -> S` whose kernel is `I`

• First Isomorphism Theorem `=> R // I ~= S`

• If `char(R) = n` and `R` is unital, then `R` contains a subring `~= ZZ // nZZ`

• `varepsilon_R: ZZ -> R, m |-> m*1`

• Since `char(R) = n`, the additive order of `1` in `(R,+)` is `n => ker(varepsilon_R) = nZZ`

• By the First Isomorphism Theorem, `ZZ // nZZ ~= ZZ // ker(varepsilon_R) ~= im(varepsilon_R)`

• If `F` is a field of `char(p)` where `p` is prime, then `F` has a subfield isomorphic to `ZZ // pZZ`, called the prime subfield of `F`

• What is the prime subfield of a field of characteristic `0`?

• By the First Isomorphism Theorem, we have a subring `~= ZZ`

• `varepsilon_R: ZZ -> F`

• Since `char(R) = 0`, the additive order of `1` in `F` is `oo`

• Therefore, `varepsilon_R` is injective, so `ZZ` is a subring of `F`

Field of Fractions

• Rational numbers can be thought of as tuples `(a,b)` where `a in ZZ, b in ZZ \\ {0}`

• For instance, `6/3 = 2/1`, so `(6,3) ~ (2,1)`

• We have to put an equivalence relation on `ZZ oplus ZZ \\ {0}`

• The relation is `(a,b) ~ (c,d) <=> ad - bc = 0`

Let's check that `~` defines an equivalence relation on `ZZ oplus ZZ \\ {0}`

Reflexive: We must check that `(a,b) ~ (a,b)` `AA a,b in ZZ oplus ZZ \\ {0}`

`(a,b) ~ (a,b) <=> ab - ba = 0`

Since `ab - ba = 0 => (a,b) ~ (a,b)`

Symmetric: We must check that if `(a,b) ~ (c,d)`, then `(c,d) ~ (a,b)`

Assume `(a,b) ~ (c,d) <=> ad - bc = 0`

`(c,d) ~ (a,b) <=> cb - da = 0`

Since `ad - bc = 0 => (c,d) ~ (a,b)`

Transitive: Suppose `(a,b) ~ (c,d)` and `(c,d) ~ (e,f)`

We claim `(a,b) ~ (e,f)`. We must show `af - be = 0`

`(a,b) ~ (c,d) => ad - bc = 0 => ad = bc`

`(c,d) ~ (e,f) => cf - de = 0 => cf = de`

`=> adcf = bcde => cd(af - be) = 0`

Either `cd = 0 or cd != 0`

If `cd = 0, d != 0 => c = 0`

`ad = bc = b*0 = 0`

`d != 0 => a = 0`

`0*f = cd = de = 0`

`d != 0 => e = 0`

`af - be = 0 - 0 = 0`

• We now define addition and multiplication on `ZZ oplus ZZ \\ {0} // ~`

We define addition by `(a,b) + (c,d) = (ad + bc, bd)`

We must check that this is well-defined

Suppose `(a_1,b_1) ~ (a_2,b_2)` and `(c_1,d_1) ~ (c_2,d_2)`

We claim `(a_1d_1 + b_1c_1, b_1d_1) ~ (a_2d_2 + b_2c_2, b_2d_2)`

`<=> a_1d_1b_2d_2 + b_1c_1b_2d_2 - (a_2d_2b_1d_1 + b_2c_2b_1d_1) = 0`

`(a_1,b_1) ~ (a_2,b_2) <=> a_1b_2 - b_1a_2 = 0`

`(c_1,d_1) ~ (c_2,d_2) <=> c_1d_2 - c_2d_1 = 0`

Since `a_1b_2 - b_1a_2 = 0` and `c_1d_2 - c_2d_1 = 0`

`=> d_1d_2(a_1b_2 - b_1a_2) + b_1b_2(c_1d_2 - c_2d_1) = 0`

Therefore, `(a_1d_1 + b_1c_1, b_1d_1) ~ (a_2d_2 + b_2c_2, b_2d_2)`

Now we check that multiplication is well-defined

We define `(a,b) * (c,d) = (ac,bd)`

Suppose `(a_1,b_1) ~ (a_2,b_2)` and `(c_1,d_1) ~ (c_2,d_2)`

We claim `(a_1c_1, b_1d_1) ~ (a_2c_2, b_2d_2) <=> a_1c_1b_2d_2 - b_1d_1a_2c_2 = 0`

Since `(a_1,b_1) ~ (a_2,b_2) <=> a_1b_2 - b_1a_2 = 0`

`(c_1,d_1) ~ (c_2,d_2) <=> c_1d_2 - c_2d_1 = 0`

`(a_1b_2 - b_1a_2)(c_1d_2 - c_2d_1) = 0`

`a_1b_2c_1d_2 - b_1a_2c_1d_2 + b_1a_2c_2d_1 - a_1b_2c_2d_1 + (b_1a_2c_2d_1 - b_1a_2c_2d_1) = 0`

`(a_1b_2c_1d_2 - b_1a_2c_2d_1) + b_1a_2(c_2d_1 - c_1d_2) + c_2d_1(b_1a_2 - a_1b_2) = 0`

`=> (a_1b_2c_1d_2 - b_1a_2c_2d_1) = 0`

• Given any integral domain, we define the field of fractions, `Q(A)` to be `A oplus A \\ {0} // ~`

Proposition: Given an integral domain `R` and an injective unital ring homomorphism `phi: R -> K` where `K` is a field, the map `phi` extends uniquely to a unital ring homomorphism `bar phi: Q(R) -> K, bar phi((r,1)``) = phi(r)`

We first prove uniqueness of `bar phi`

Suppose `bar phi, psi` are ring homomorphisms extending `phi`. We claim `bar phi = psi`

`bar phi((r,1)``) = phi(r) = ``psi((r,1)``)`

Since both are ring homomorphisms,

`bar phi((a,b)``) = bar phi((a,1)``, (1,b)) = bar phi((a,1)``) * bar phi((1,b)``) = phi(a) * bar phi((1,b)``)`

`psi((a,b)``) = psi((a,1)``, (1,b)) = psi((a,1)``) * psi((1,b)``) = phi(a) * psi((1,b)``)`

Therefore, it suffices to show that `psi((1,b)``) = bar phi((1,b)``)` `AA b in ZZ \\ {0}`

We show that both are multiplicative inverses of `phi(b)`

Notice `psi((1,b)``) * psi((b,1)``) = psi((1,b)(b,1)) = psi((b,b)``) = 1`

`=> psi((1,b)``)` is the multiplicative inverse of `psi((b,1)``) = phi(b)`

`bar phi((1,b)``) * bar phi((b,1)``) = bar phi((1,b)(b,1)) = bar phi((b,b)``) = 1`

`=> bar phi((1,b)``)` is the multiplicative inverse of `bar phi((b,1)``) = phi(b)`

`=> psi((1,b)``) = bar phi((1,b)``)`` = phi(b)^-1`

Therefore, `bar phi` is unique

Now we prove existence

If `bar phi` exists, it must be defined as `bar phi((a,b)``)`` = phi(a)phi(b)^-1`

Let's show that `bar phi` is well-defined

Suppose `(a_1,b_1) ~ (a_2,b_2) <=> a_1b_2 = b_1a_2`

We claim `bar phi((a_1,b_1)``) = bar phi((a_2,b_2)``)` `<=> phi(a_1)phi(b_1)^-1 = phi(a_2)phi(b_2)^-1`

Since `a_1b_2 = b_1a_2 => phi(a_1b_2) = phi(b_1a_2) => phi(a_1)phi(b_2) = phi(b_1)phi(a_2)`

`b_1, b_2 != 0, phi` injective `=> phi(b_1), phi(b_2) != 0 =>` they are units

Multiply `phi(a_1)phi(b_2) = phi(a_2)phi(b_1)` by `phi(b_1)^-1phi(b_2)^-1`

to get `phi(a_1)phi(b_1)^-1 = phi(a_2)phi(b_2)^-1`

We must check that `bar phi` is a ring homomorphism

Let `(a,b), (c,d) in Q(R)`

`bar phi((a,b) + (c,d)) = bar phi((ad + bc, bd)``)`

`= phi(ad + bc)phi(bd)^-1 = phi(a)phi(d)phi(b)^-1phi(d)^-1 + phi(b)phi(c)phi(b)^-1phi(d)^-1`

`= phi(a)phi(b)^-1 + phi(c)phi(d)^-1 = bar phi((a,b)``) + bar phi((c,d)``)`

`bar phi((a,b)(c,d)``) = phi((ac,bd)``)`` = phi(ac)phi(bd)^-1 = phi(a)phi(c)phi(b)^-1phi(d)^-1`

`= (phi(a)phi(b)^-1)(phi(c)phi(d)^-1) = bar phi((a,b)``) bar phi((c,d)``)`

`a != 0, bar phi((a,a)``)`` = phi(a)phi(a)^-1 = 1 => bar phi` is a unital ring homomorphism

`bar phi((a,b)``)`` = 0 => phi(a)phi(b)^-1 = 0 => phi(a) = 0 => a = 0 => bar phi` is injective

• Suppose `F` is a field of characteristic `0`. What is the prime subfield of `F`?

• We've seen that we have an injective unital ring homomorphism `varepsilon_F: ZZ -> F`

• By the proposition, `EE!` `phi: Q(ZZ) ~= QQ -> F =>` the prime subfield of `F` when `char(F) = 0` is `QQ`

• Every field either contains `QQ` or `ZZ // pZZ` for some prime `p`

Polynomial Rings

• Definition: Let `R` be a commutative ring. The polynomial ring `R[x]` of polynomials over `R` in the indeterminate `x` is defined to be the ring consisting of all expressions of the form `sum_(i=0)^n a_ix^i = a_nx^n + a_(n-1)x^(n-1) + ... + a_1x + a_0`, `a_i in R, n in ZZ^(>= 0)`

• We can always write an element of `R[x]` as `sum_(i=0)^n a_ix^i` where `a_n != 0`

• If we have two polynomials `sum_(i = 0)^n a_ix^i, sum_(j = 0)^m b_jx^j` written in this form then `sum_(i = 0)^n a_ix^i = sum_(j = 0)^m b_jx^j <=> n = m` and `a_k = b_k` `AA 1 <= k <= n`

• Note: `x` and `x^2` take on the same values at all elements of `ZZ // 2ZZ` but `x != x^2` as elements of `ZZ // 2ZZ [x]`

• Addition and multiplication are defined exactly as how they were in grade school, except if the coefficient ring `R` has `char(R) = n`, then we have to reduce `mod n`

• `(3x^2 + 2x + 1) + (x + 4) = 3x^2 + 3x + 5`

• `= 3x^2 + 3x + 0` if in `[ZZ]_5`

• Definition: Let `f(x) = sum_(i = 0)^n a_ix^i in R[x]`. If `a_n != 0`, then the degree of `f`, denoted by `deg(f(x))`, is `n`. The leading term is `a_n`. If `a_n = 1`, then `f(x)` is said to be monic. If `f(x) = r in R`, then `f(x)` is constant. `R` is called the coefficient ring.

Proposition: If `R` is an integral domain, then `R[x]` is an integral domain

Let `sum_(i = 0)^n a_ix^i, sum_(j = 0)^m b_jx^j in R[x]` be nonzero elements `s.t.` the leading terms are `a_n, b_m != 0`

Then the product has leading term `a_nb_m`

`a_nb_m != 0` since `R` is a domain and `a_n, b_m != 0`

Therefore, the product is nonzero

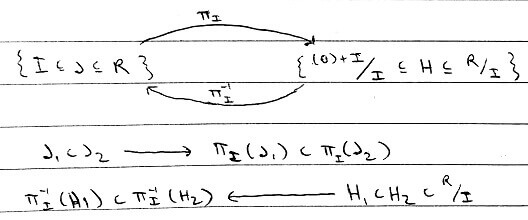
• For a unital commutative ring `R`, if every ideal of `R` is finitely generated `<=>` every ideal of `R[x]` is finitely generated

• Degree adds under taking products in `R[x]` when `R` is a domain

• `ZZ // 4ZZ: f(x) = [2]_4x + [1]_4, g(x) = [2]_4x^2 + [2]_4x`

• `f(x)g(x) = [4]_4x^3 + [4]_4x^2 + [2]_4x^2 + [2]_4x = [2]_4x^2 + [2]_4x`

• `deg(fg) != deg(f)deg(g)`

• Unexpected things happen in `R[x]` when `R` is not a domain

• However, when `F` is a field, none of this occurs

• Even better, we have a division algorithm in `F[x]` like the one in `ZZ`

• We can order collections of elements in `F[x]` by their degrees

• In `ZZ`: If `a in ZZ, b != 0 in ZZ`, then `EE q, r in ZZ` `s.t.` `a = bq + r` `0 <= r < |b|`

Division Algorithm in `F[x]`: Let `F` be a field. Let `f(x) in F[x]`. Let `g(x) != 0 in F[x]`. Then `EE q(x), r(x)` `s.t.` `f(x) = g(x)q(x) + r(x)` where either `0 <= deg(r(x)) < deg(g(x))` or `r(x) = 0`

First we prove existence

If `f(x) = 0`, take `q(x) = 0` and `r(x) = 0`

If `deg(g(x)) > deg(f(x))`, let `q(x) = 0, r(x) = f(x)`

`f(x) = g(x)*0 + f(x), 0 <= deg(r(x)) = deg(f(x)) < deg(g(x))`

We've reduced to the case where `deg(f(x)) >= deg(g(x))`

We induct on `deg(f(x)) = n`

Base Case: `n = 0`. In this case `f(x)` is constant, and since `deg(g(x)) <= deg(f(x)) = 0 => deg(g(x)) = 0 => g(x)` is a constant

`f(x)` is constant `=> f(x) = a in F \\ {0}`

`g(x)` is constant `=> g(x) = b in F \\ {0}`

`a = b*(a/b)`. Let `q(x) = a/b`. Let `r(x) = 0`

Inductive Hypothesis: Suppose for some `n >= 0, k <=n` `AA k in ZZ^(>= 0).` If `f(x)` is a polynomial of degree `k`, then `EE q(x), r(x)` `s.t.` `f(x) = g(x)q(x) + r(x)` where `0 <= deg(r(x)) < deg(g(x))` or `r(x) = 0`

WTS: If `f(x)` is a polynomial of degree `n+1` in `F[x]`, then `EE q(x), r(x)` `s.t.` `f(x) = g(x)q(x) + r(x)` where `0 <= deg(r(x)) < deg(g(x))` or `r(x) = 0`

Let `a_n` be the leading term of `f(x)`, `b_m` be the leading term of `g(x)`

The leading monomial of `f(x)` is `a_nx^n` and the leading monomial of `g(x)` is `b_mx^m`, `m <= n`

Consider `f(x) - a_nb_m^-1x^(n-m)g(x)`. This has degree `< deg(f(x)) = n+1`

So the inductive hypothesis applies to `f(x) - a_nb_m^-1x^(n-m)g(x)`

`EE q_1(x), r_1(x) in F[x]` `s.t.` `(f(x) - a_nb_m^-1x^(n-m)g(x)) = g(x)q_1(x) + r_1(x)` where `0 <= deg(r_1(x)) < deg(g(x))` or `r_1(x) = 0`

Rearranging this, we find `f(x) = g(x)(a_nb_m^-1x^(n-m) + q_1(x)) + r_1(x)` where `0 <= deg(r_1(x)) < deg(g(x))` or `r_1(x) = 0`

Now we prove uniqueness

Suppose `f(x) = g(x)q_1(x) + r_1(x) = g(x)q_2(x) + r_2(x)`

`g(x)q_1(x) + r_1(x) - g(x)q_2(x) - r_2(x) = 0`

`g(x)(q_1(x) - q_2(x)) = (r_2(x) - r_1(x)) => g(x) | (r_2(x) - r_1(x))`

`deg(r_2(x) - r_1(x)) <= max{deg(r_1(x)), deg(r_2(x))} < deg(g(x))`

If `r_2(x) - r_1(x) != 0`, then that is a contradiction

`deg(g(x)) > deg(f(x))`

If `g(x) | f(x) => EE q(x) in F[x]` `s.t.` `g(x)q(x) = f(x)`

`deg(g(x)) + deg(q(x))` (which is `>= 0`) `= deg(f(x)) < deg(g(x))`, a contradiction

So we must have `r_1(x)- r_2(x) = 0`

Since `F[x]` is an integral domain, we see that `q_1(x) = q_2(x)`

• If `R` is an integral domain, then we can make sense of `f(x) | g(x).` This means that `EE q(x) in R[x]` `s.t.` `f(x)q(x) = g(x)`

• `f(x)` is called a factor of `g(x)`. `a in R` is called the root of `f(x)` if `f(a) = 0`

• Let `a in R`. Then `a` is called a zero of multiplicity `n` of `f(x)` if `(x-a)^n | f(x)` and `(x-a)^(n+1) cancel(|) f(x)`

Exercise: Show that if `R` is an integral domain, the only units of `R[x]` are the units of `R`

Suppose `f(x) != 0` is a unit in `R[x]`. Then there exists `g(x) != 0` in `R[x]` `s.t.` `f(x)g(x) = 1`

`deg(f(x)g(x)) = deg(f(x)) + deg(g(x)) = deg(1) = 0`

`=> deg(f(x)) = 0 => f(x) in R`

Theorem: A polynomial of degree `n` over a field `F` has at most `n` roots in `F`

Base Case: If `n = 0`, then `f(x) in F \\ {0}`, so it has `0` roots

Inductive Hypothesis: Suppose for some `n >= 0, k <= n` `AA k in ZZ^(>= 0)` If `f(x)` is a polynomial of degree `k`, then `f(x)` has at most `k` roots in `F`

WTS: If `f(x)` is a polynomial of degree `n+1`, then `f(x)` has at most `n+1` roots in `F`

Let `f(x)` be a polynomial of degree `n+1`. If `f(x)` has no roots in `F`, then the statement is proven

Therefore we can assume `f(x)` has a root, call it `alpha in F`

Let `h` be the multiplicity of `alpha`. We can write `f(x) = (x-alpha)^hq(x)` where `(x-alpha) cancel(|) q(x)`

If `alpha` is the only root, then `h <= n + 1` and the statement is proven

Suppose that `beta` is a root of `f(x), beta != alpha`

`0 = f(beta) = (beta - alpha)^hq(beta) => q(beta) = 0`

Therefore, `beta` is a root of `q(x)`

We claim that the multiplicity of `beta` as a root of `q(x)` is equal to the multiplicity of `beta` as a root of `f(x)`

Since `beta` is a root of `q(x) => (x - beta) | q(x)`

Let `m_1` be the multiplicity of `beta` as a root of `q(x)` (So `(x-beta)^(m_1) | q(x)` and `(x - beta)^(m_1+1) cancel(|) q(x)`)

Since `beta` is a root of `f(x)`, we can write `f(x) = (x - beta)^(m_2)q_2(x)`

`m_2`: the multiplicity of `beta` as a root of `f(x)`

`q(x) = (x - beta)^(m_1)q_1(x)`

Notice `f(x) = (x - alpha)^nq(x) = (x - alpha)^h(x - beta)^(m_1)q_1(x)`

`f(x) = (x - beta)^(m_2)q_2(x)`. We claim `m_1 = m_2`

Case 1: `m_1 > m_2`. `(x - alpha)^h(x - beta)^(m_1)q_1(x) - (x - beta)^(m_2)q_2(x) = 0`

Since `F[x]` is a domain, `(x - alpha)^h(x - beta)^(m_2 - m_1)q_1(x) - q_2(x) = 0`

Plugging in `beta` gives `q_2(beta) = 0`, which is a contradiction

Case 2: `m_1 < m_2`. (x - alpha)^h(x - beta)^(m_1)q(x) = (x - beta)^(m_2)q_2(x)`

`(x - alpha)^h(x- beta)^(m_1)q_1(x) - (x - beta)^(m_2)q_2(x) = 0`

Since `F[x]` is a domain, `(x - alpha)^hq_1(x) - (x - beta)^(m_2 - m_1)q_2(x) = 0`

Plugging in `beta => q_1(beta) = 0`, which is a contradiction

Therefore, `m_1 = m_2`

By the induction hypothesis, since `deg(q(x)) < deg(f(x)) = n + 1, q(x)` has at most `deg(q(x)) = n + 1 - h` roots counted with multiplicity

Since the remaining roots of `f(x)` are exactly the roots of `q(x)` with the same multiplicity, since `f(x) = (x - alpha)^hq(x)` we see that `f(x)` has at most `h + deg(q(x)) = h + n + 1 - h = n + 1` roots in `F`

• Why "at most"? Ex: `x^2 + 1 in RR[x]` has no roots

Theorem: `F[x]` is a principal ideal domain

Let `I` be a nonzero proper ideal of `F[x]`. Let `f(x) != 0` be an element of minimal degree in `I`

Since `I` is proper, the degree of `f(x)` must be positive

(If `deg(f(x)) = 0 => f(x) in F \\ {0} => f(x)` is a unit in `I => I = F[x]`)

Let `g(x) in I`. By the division algorithm, `EE q(x), r(x) in F[x]` `s.t` `g(x) = f(x)q(x) + r(x)` where `0 <= deg(r(x)) < deg(f(x))` or `r(x) = 0`

We can rewrite this as `r(x) = g(x) - f(x)q(x) in I`

Since `F` was chosen to have minimal degree, `r(x) = 0 => I sube (f(x))`

Since `f(x) in I => (f(x)) sube I => (f(x)) = I`

Exercise: Let `R` be a commutative ring with unity. Let `I sube R` be an ideal. Show that `I[x]` = the set of polynomials in `R[x]` whose coefficients lie in `I` is an ideal of `R[x]`

We must show that `I[x]` is a subgroup. Let `f(x) = sum_(i = 0)^n a_ix^i, g(x) = sum_(j = 0)^m b_jx^j in I[x]`

WLOG, `n >= m`

`f(x) - g(x) = sum_(k = 0)^n c_kx^k` where `c_k = {(a_k - b_k if k <= m), (a_k if m < k <= n):}`

`a_k - b_k in I` since `a_k, b_k in I` and `I` is an ideal (for `0 <= k <= m`)

`a_k in I` if `m < k <= n =>` By definition, `f(x) - g(x) in I[x]`

It suffices to show that `AA` monomials `r_hx^h in R[x]`, `AA f(x) in I[x], r_hx^h - f(x) in I[x]`

Let `f(x) = sum_(i = 0)^n a_ix^i`. Then `r_hx^h(sum_(i = 0)^n a_ix^i) = sum_(j = h)^(n+1) r_ha_j - hx^j in I[x]`

Let `sum_(k = 0)^m r_kx^k in R[x], f(x) in I[x]`

Then `sum_(k = 0)^m r_kx^k*f(x) = sum_(k = 0)^m (r_kx^kf(x)) in I[x]`

Since `I[x]` is a subgroup `=> sum_(k = 0)^m r_kx^kf(x) in I[x]`

Ex: If `p` is a prime ideal in `R`, then `p[x]` is a prime ideal in `R[x]`

We show that `R[x] // p[x]` is an integral domain

To do this, we exhibit an isomorphism `R[x] // p[x] ~= R // p [x]`

`pi_p: R -> R // p`

There is a map of rings `bar pi_p: R[x] -> R // p [x], sum_(i = 0)^n a_ix^i |-> sum_(i = 0)^n pi_p(a_i)x^i`

(Surjective): Fix `sum_(j = 0)^m (b_i + p)x^i in R // p [x]`

Notice `bar pi_p(sum_(j = 0)^m b_jx^j) = sum_(j = 0)^m pi_p(b_j)x^j = sum_(j= 0)^m (b_j + p)x^j`

`bar pi` is onto `R[x] -> R // p [x]`

We claim `ker(bar pi_p) = p[x]`

`(sube)` Let `sum_(i = 0)^n a_ix^i in ker(bar pi_p) => bar pi_p(sum_(i = 0)^n a_ix^i) = sum_(i = 0)^n pi_p(a_i)x^i = 0`

`=> pi_p(a_i) = 0` `AA i`

`a_i + p = 0 + p => a_i in p` `AA i =>` since all `a_i in p => sum_(i = 0)^n a_ix^i in p[x]`

`(supe)` Suppose `sum_(i = 0)^m c_ix^i in p[x] => c_i in p` `AA i`

`bar pi_p(sum_(i = 0)^m c_ix^i) = sum_(i = 0)^m pi_p(c_i)x^i = sum_(i = 0)^m (c_i + p)x^i = sum_(i = 0)^m (0 + p)x^i = 0`

`=> sum_(i = 0)^m c_ix^i in ker(bar pi_p)`

Since `bar pi_p: R[x] -> R // p [x]` is surjective and `ker(bar pi_p) = p[x]`, by the First Isomorphism Theorem, `R[x] // p[x] ~= R // p [x]`

`R // p [x]` is a domain `<=> R[x] // p[x]` is a domain `<=> p[x]` is prime

However, if `m` is a maximal ideal of `R`, `m[x]` need not be a maximal ideal of `R[x]`

Let `R = ZZ, m = pZZ`, `p` prime

Then `ZZ[x] // pZZ[x] ~= ZZ // pZZ [x]`

We know that `ZZ // pZZ [x]` is not a field `<=> pZZ[x]` is not maximal

• What is the right generalization of a prime number in `F[x]`?

• `p in ZZ` is prime `<=>` whenever `p = ab, a = +- p, b = +- p` or vice versa

• Definition: Let `R` be an integral domain. Let `f(x) in R[x]` which is nonzero and not a unit. `f(x)` is irreducible if whenever `f(x) = g(x)h(x)` for some `g(x), h(x) in R[x]`, either `g(x)` or `h(x)` must be a unit. If an element is not a unit, nonzero, and not irreducible, it is reducible

• Re-examining the definition of irreducible polynomials, since `R` is a domain, the units of `R[x]` are the units of `R` itself, so we can rephrase the definition as:

• `f(x)` is irreducible if whenever `f(x) = g(x)h(x)` for some `g(x), h(x) in R[x]` we must have `g(x)` or `h(x)` is a unit in `R`

• When `R` is a field, we can say even more

Proposition: Let `F` be a field. Then an element `f(x) in F[x]` (nonzero, non-unit) is irreducible if and only if we cannot express `f(x)` as a product of two polynomials whose degrees are `< deg(f(x))`

`(=>)` Suppose that `f(x)` is irreducible. Suppose for a contradiction that `f(x) = g(x)h(x)` where `deg(g(x)), deg(h(x)) < deg(f(x))`

Since `f(x)` is irreducible, one of `g(x)` or `h(x)` must be a unit in `F`

If `g(x) in F^x`, then `deg(g(x)) = 0`

`f(x) = g(x)h(x) => deg(f(x)) = cancel(deg(g(x))) + deg(h(x)) => deg(f(x)) = deg(h(x))`, which is a contradiction

`(lArr)` Suppose that `f(x)` is such that `f(x)` cannot be factored as a product `f(x) = g(x)h(x)` where `deg(g(x)), deg(h(x)) < deg(f(x))`

We claim that `f` is irreducible

Suppose `f(x) = p(x)q(x)`

By assumption, either `deg(p(x)) = deg(f(x))` or `deg(q(x)) = deg(f(x))`

In the first case, `deg(q(x)) = 0 <=> q(x) in F^x`

In the second case, `deg(p(x)) = 0 <=> p(x) in F^x`

Therefore, `f` is irreducible

Proposition: If `R` is a principal ideal domain, then every prime ideal is maximal

`(lArr)` maximal ideals are always prime in integral domains

`(=>)` Suppose that `p` is a prime ideal. Let `p in I` where `I` is an ideal

We claim that `I = p` or `I = R`

Since `R` is a principal ideal domain, `EE x, z in R` `s.t.` `(x) = p, (z) = I, (x) sube (z)` where `(x)` is prime

Since `(x) sube (z), EE y in R` `s.t.` `x = yz => yz in (x)`

Since `(x)` is a prime ideal, either `y in (x)` or `z in (x)`

If `y in (x) => EE r in R` `s.t.` `y = rx`

Then `x = yz = rxz = (rz)x`

Since `R` is a domain `=> rz = 1 => z in R^x => (z) = R`

If `z in (x)`, then `(z) sube (x)` and therefore `(z) = (x)`

`=> p = (x)` is maximal

• Since `F(x)` is a principal ideal domain, to show that irreducible polynomials generate maximal ideals, it suffices to show that irreducible polynomials generate prime ideals

• To do this, we must establish some properties of irreducible polynomials

• The property we want is: If `f(x)` is irreducible, then `f(x) | g(x)h(x) => f(x)|g(x)` or `f(x)|h(x)`

• Definition: Let `f(x), g(x) in F[x]`. A polynomial `h(x)` is a greatest common divisor of `f(x)` and `g(x)` if

• 1) `h(x) | f(x)` and `h(x) | g(x)`

• 2) If `q(x)` is any other common divisor of `f(x)` and `g(x)`, then `q(x) | h(x)`

• We used "a" and not "the" because if `h(x)` satisfies these conditions, so does `c*h(x)` `AA c in F^x`

• Suppose `h_1(x), h_2(x)` both satisfy these conditions.

• Then `h_1(x) | h_2(x) => EE p_1(x) in F[x]` `s.t.` `h_1(x)p_1(x) = h_2(x)`

• And `h_2(x) | h_1(x) => EE p_2(x) in F[x]` `s.t.` `h_2(x)p_2(x) = h_1(x)`

• `h_2(x) = h_1(x)p_1(x) = h_2(x)p_2(x)p_1(x)`

• Since `F[x]` is a domain, `p_2(x)p_1(x) = 1 => p_2(x), p_1(x) in F^x`

• From now on, "the greatest common divisor" means the unique polynomial `h(x)` satisfying these conditions of the definition which is monic

The greatest common divisor of `f(x)` and `g(x)` is the monic generator of `(f(x), g(x))`

Let `f(x), g(x) in F[x]` `s.t.` at least one of them is nonzero

Consider `(f(x), g(x)) sube F[x]`

Since `F[x]` is a principal ideal domain, `(f(x), g(x))` is generated by a single element

Let `h(x)` be the monic generator of `(f(x), g(x))`

Notice that since `f(x), g(x) in (h(x)) => h(x)|f(x), h(x)|g(x)`

Since `h(x) in (f(x), g(x)) => EE r(x), s(x) in F[x]` `s.t.` `h(x) = r(x)f(x) + s(x)g(x)`

Let `q(x)` be a common divisor of `f(x)` and `g(x)`

Then `EE p_1(x), p_2(x) in F[x]` `s.t.` `q(x)p_1(x) = f(x), q(x)p_2(x) = g(x)`

Substituting, we find `h(x) = r(x)q(x)p_1(x) + s(x)q(x)p_2(x) => q(x)|h(x)`

Therefore, `h(x)` is the gcd of `f(x)` and `g(x)`

• We've shown that `gcd(f(x), g(x))` can be written as an `F[x]` linear combination of `f(x)` and `g(x)`

Proposition: Suppose that `f(x)` is irreducible in `F[x]`. Then `f(x)|g(x)h(x) => f(x)|g(x)` or `f(x)|h(x)`, `AA g(x), h(x) in F[x]`

Suppose that `f(x)` is irreducible and `f(x) cancel(|) g(x)`. We claim `f(x)|h(x)`

First we show `gcd(f(x), g(x)) = 1`

Suppose `q(x)|f(x)` and `q(x)|g(x)`

If `q(x)|f(x)` then since `f(x)` is irreducible, `q(x) = c*f(x)` for some unit `c in F^x`, or `q(x) in F^x`

If `q(x) = c*f(x)` and `q(x)|g(x)`, then `c*f(x)|g(x) => f(x)|g(x)`, which is a contradiction

`=> q(x) in F^x`

Therefore, `gcd(f(x), g(x)) = 1`

By what we just proved, `EE r(x), s(x) in F[x]` `s.t.` `1 = r(x)f(x) + s(x)g(x)`

Since `f(x)|g(x)h(x) => EE q'(x) in F[x]` `s.t.` `f(x)q'(x) = g(x)h(x)`

`f(x)q'(x)*1 = f(x)q'(x)*(r(x)f(x) + s(x)g(x)) = g(x)h(x)`

`g(x)h(x) = f(x)q'(x)r(x)f(x) + f(x)q'(x)s(x)g(x)`

`= g(x)h(x)r(x)f(x) + f(x)q'(x)s(x)g(x)`

`=> h(x) = f(x)*(h(x)r(x) + q'(x)s(x)) => f(x)|h(x)`

Proposition: If `f(x) in F[x]` is irreducible, then `(f(x))` is prime

Let `g(x), h(x) in F[x]` `s.t.` `g(x)h(x) in (f(x)) => f(x)|g(x)h(x)`

By what we just showed, `f(x)` is irreducible implies `f(x)|g(x)h(x) => f(x)|g(x)` `(g(x) in (f(x)))` or `f(x)|h(x)` `(h(x) in (f(x))`

• We care about irreducible polynomials because they generate the maximal ideals of `F[x]`

We just have to show that having the property `f(x)|g(x)h(x) => f(x)|g(x)` or `f(x)|h(x)` is equivalent to being irreducible

Suppose `f(x) in F[x]` `s.t.` whenever `g(x), h(x) in F[x]` `s.t.` `f(x)|g(x)h(x) => f(x)|g(x)` or `f(x)|h(x)`

We claim `f(x)` is irreducible

Suppose `f(x) = p(x)q(x)`. We claim that either `p(x) in F^x` or `q(x) in F^x`

Since `f(x)*1 = p(x)q(x) => f(x)|p(x)q(x)`

By assumption, `f(x)|p(x)` or `f(x)|q(x)`

`f(x)|p(x) => EE p'(x) in F[x]` `s.t.` `f(x)p'(x) = p(x)`

`f(x) = f(x)p'(x)q(x) => q(x) in F^x`

`f(x)|q(x) => EE q'(x) in F[x]` `s.t.` `f(x)q'(x) = q(x)`

`f(x) = f(x)p(x)q'(x) => p(x) in F^x`

• Every maximal ideal is of the form `(f(x))` where `f(x)` is irreducible `// F`

• There are conditions that imply irreducibility or reducibility

• The first condition applies to any field, but only to degree `2` or degree `3` polynomials

Proposition: Let `F` be a field. `f(x) in F[x]` is irreducible `// F <=> f(x)` has no roots

`(=>)` Suppose `f(x)` is irreducible. Then since `cancel(EE)` a factorization `f(x) = g(x)h(x)` where `deg(g(x)), deg(h(x)) < deg(f(x))`, `f` has no linear factors `<=> f(x)` has no roots in `F`

`(lArr)` Suppose `f(x)` has no roots in `F <=> f(x)` has no linear factors

Suppose `deg(f(x)) = 2`

Suppose for a contradiction that `f(x)` is reducible `=> EE g(x), h(x) in F[x]` `s.t.` `f(x) = g(x)h(x) in F[x]` where `deg(g(x)), deg(h(x)) < 2`

`=> deg(g(x)) = deg(h(x)) = 1`, which is a contradiction*

Suppose `deg(f(x)) = 3`

Suppose for a contradiction that `f(x)` is reducible `=> EE g(x), h(x) in F[x]` `s.t.` `f(x) = g(x)h(x) in F[x]` where `deg(g(x)), deg(h(x)) < 3`

`=>` either `deg(g(x)) = 2` and `deg(h(x)) = 1`, which is a contradiction*, or vice versa, which is also a contradiction*

*contradiction because `f(x)` has no linear factors

• Definition: Let `f(x) in ZZ[x]`. The content of `f(x)` is the greatest common divisor of the coefficients of `f(x)`. If the content is `1`, then `f(x)` is primitive

• Ex: Monic polynomials are primitive

Proposition: If `f(x), g(x)` are primitive, then `f(x)g(x)` is primitive

We prove the contrapositive. Suppose `f(x), g(x) in ZZ[x]` `s.t.` `f(x)g(x)` is not primitive

Then `EE p in ZZ^+` prime such that `p|content(f(x)g(x)) => EE q(x) in ZZ[x]` `s.t.` `f(x)g(x) = p(q(x)) in pZZ[x]`

We've already seen that `pZZ` is a prime ideal of `ZZ[x]`

Thus `f(x)g(x) in pZZ[z] => f(x) in pZZ[x]` or `g(x) in pZZ[x]`

`=> p|content(f(x))` or `p|content(g(x)) =>` either `f(x)` or `g(x)` is not primitive

Gauss's Lemma: If `f(x) in ZZ[x]` is reducible over `QQ`, then `f(x)` is reducible over `ZZ`

Suppose that `f(x)` is reducible over `QQ`

Then `EE g(x), h(x) in QQ[x]` `s.t.` `f(x) = g(x)h(x)`

We can harmlessly divide through by the content of `f(x)` to assume that `f(x)` is primitive

Let `alpha` be the least common multiple of the denominators in `g(x)`. Let `beta` be the least common multiple of the denominators in `h(x)`

Thus, `alpha*g(x) in ZZ[x], beta*h(x) in ZZ[x]`

So we have a factorization `alpha beta f(x) = alpha g(x) * beta h(x) in ZZ[x]`

Notice that the content of `alpha beta f(x)` is `alpha beta`

Let `c_g` be the content of `alpha g(x)`, `c_h` be the content of `beta h(x)`

Notice that `(alpha g(x)) / c_g` and `(beta h(x)) / c_h` are primitive

We can write `alpha beta f(x) = c_(g) ((alpha g(x)) / c_g) * c_h ((beta h(x)) / c_h)`

Since `(alpha g(x)) / c_g, (beta h(x)) / c_h` are primitive, the content of the right side is `c_g*c_h`

The content of the left side is `alpha beta => alpha beta = c_gc_h`

Therefore `(alpha beta)/(c_gc_h) f(x) = f(x) = (alpha g(x)) / c_g * (beta h(x)) / c_h` where `(alpha g(x)) / c_g, (beta h(x)) / c_h in ZZ[x]`

Proposition: Suppose that `f(x) in ZZ[x]` `s.t.` `deg(f(x)) >= 1`. Let `p` be a prime number. Let `bar pi_p: ZZ[x] -> ZZ // pZZ[x]` be the ring homomorphism which reduces coefficients modulo `p`. If `bar pi_p(f(x))` is irreducible over `ZZ // pZZ` and `deg(bar pi_p(f(x))) = deg(f(x))`, then `f(x)` is irreducible over `QQ`

Let `f(x) in ZZ[x]` and let `p` be a prime number `s.t.` `bar pi_p(f(x))` is irreducible and `deg(bar pi_p(f(x))) = deg(f(x))`

Suppose for a contradiction that `f` is reducible over `QQ`

`=> EE g(x), h(x) in QQ[x]` `s.t.` `f(x) = g(x)h(x)` where `deg(g(x)), deg(h(x)) < deg(f(x))`

Divide through by `content(f)`. Then if `alpha` is the `lcm` of the denominators of `g(x)` and `beta` is the `lcm` of the denominators of `h(x)`, then `alpha g(x), beta h(x) in ZZ[x]`

Let `c_g, c_h` denote the content of `alpha g(x), beta h(x)`

Then `f(x) = (alpha g(x)) / c_g * (beta h(x)) / c_h`

Notice that `deg((alpha g(x)) / c_g) = deg(g(x))` and `deg((beta h(x)) / c_h) = deg(h(x))`

Reducing `mod p`, we see that `bar pi_p(f(x)) = bar pi_p((alpha g(x)) / c_g) bar pi_p((beta h(x)) / c_h)`

By assumption, `bar pi_p(f(x))` is irreducible `=>` either `deg(bar pi_p((alpha g(x)) / c_g)) = 0` or `deg(bar pi_p((beta h(x)) / c_h)) = 0`

`=> deg(bar pi_p((beta h(x)) / c_h)) = deg(bar pi_p(f(x)))` or `deg(bar pi_p((alpha g(x)) / c_g))) = deg(bar pi_p(f(x)))`

Since we assumed `deg(bar pi_p(f(x))) = deg(f(x))`, either `deg(bar pi_p((beta h(x)) / c_h)) = deg(f(x))` or `deg(bar pi_p((alpha g(x)) / c_g)) = deg(f(x))`

Since degree only drops or stays the same when reducing `mod p`,

1) `deg(h(x)) >= deg(bar pi_p((beta h(x)) / c_h)) = deg(f(x))`, which is a contradiction

2) `deg(g(x)) >= deg(bar pi_p((alpha g(x)) / c_g)) = deg(f(x))`, which is a contradiction

Therefore, `f` is irreducible over `QQ`

Eisenstein's Criterion: Let `f(x) = sum_(i = 0)^n a_ix^i`. Let `p` be a prime number. Suppose that `p cancel(|) a_n`, `p|a_i AA 0 <= i <= n-1`, and `p^2 cancel(|) a_0`. Then `f` is irreducible `// QQ`

Suppose `f(x) in ZZ[x]` and `p` is a prime `s.t.` `p cancel(|) a_n`, `p|a_i AA 0 <= i <= n-1`, `p^2 cancel(|) a_0`

Suppose `f` is reducible over `QQ => EE g(x), h(x) in ZZ[x]` `s.t.` `deg(g(x), h(x)) < deg(f(x))` `s.t.` `f(x) = g(x)h(x)`

Therefore, both have positive degree

Let `g(x) = sum_(j = 0)^r b_jx_j, h(x) = sum_(k = 0)^s c_kx^k`

Notice that `a_0 = b_0c_0`

Since `p|a_0` but `p^2 cancel(|) a_0`, WLOG `p cancel(|) b_0, p|c_0`

So `cc C = {l in {1, ..., s} | p cancel(|) c_l} != {0, ..., s}`

Observe that `cc C` is nonempty since `p cancel(|) a_n, a_n = b_rc_s => p cancel(|) c_s`

`cc C sub {0, ..., s}, ccC != O/`

Let `l_0` be the minimum of `cc C => AA l < l_0, p|c_l`

Notice that `a_(l_0) = b_0c_(l_0) + b_1c_(l_0-1) + ... + b_qc_(l_0-q)` where `q` is the largest index `<= r` `s.t.` `l_0-q >= 0`

Since `p|b_1c_(l_0-1) + ... + b_qc_(l_0-q)` and `p|a_(l_0) => p|b_0c_(l_0)`, since `p cancel(|) b_0 => p|c_(l_0)`, which is a contradiction

Therefore, `f` is irreducible over `QQ`

Let `p` be prime. The `p^(th)` cyclotomic polynomial, `Phi_p(x) = (x^p-1)/(x-1)` is irreducible `// QQ`

Replace `x` with `(x+1) => Phi_p(x+1) = (((x+1)^p-1)/x) = (sum_(k = 0)^p ((p),(k)) x^k - 1)/x`

`= (sum_(k = 1)^p ((p),(k)) x^k) / x = sum_(k = 1)^p ((p),(k)) x^(k-1) = sum_(k = 0)^(p-1) ((p),(k+1)) x^k`

`= ((p),(1)) + ((p),(2))x + ... + ((p),(p-1))x^(p-2) + ((p),(p))x^(p-1)`

`= p + ((p),(2))x + ... + px^(p-2) + x^(p-1)`

Therefore `Phi_p(x+1)` is irreducible by Eisenstein's criterion

If `Phi_p(x) = f(x)g(x)` where `deg(f(x)), deg(g(x)) < deg(Phi_p(x))`, then `Phi_p(x+1) = f(x+1)g(x+1)` where `deg(f(x+1)), deg(g(x+1)) < deg(Phi_p(x+1)) = deg(Phi_p(x))`

Since `Phi_p(x+1)` is irreducible, this is a contradiction

Constructing a finite field other `ZZ // pZZ`

Let `f(x)` be an irreducible polynomial of degree `n` in `ZZ // pZZ [x]`

We know that `(f(x)) sube ZZ // pZZ [x]` is a maximal ideal

So `(ZZ // pZZ[x]) / (f(x))` is a finite field

We claim that `| (ZZ // pZZ[x]) / (f(x)) | = p^n`

Any element in `(ZZ // pZZ[x]) / (f(x))` can be written as a `ZZ // pZZ` linear combination of `{1 + (f(x)), x + (f(x)), ..., x^(n-1) + f(x)}`

We're proving by induction that `x^k + (f(x)) in ZZ // pZZ` linear span of `{1 + (f(x)), ..., x^(n-1) + (f(x))}` `AA k >= n`

Base Case: `k = n`. `f(x) = x^n + a_(n-1)x^(n-1) + ... + a_1x + a_0 in ZZ // pZZ[x]`

`x_n + a_(n-1)x^(n-1) + ... + a_0 + (f(x)) = 0 + (f(x))`

`x_n + (f(x)) = -a_(n-1)x^(n-1) - ... - a_0 + (f(x))`

Inductive Hypothesis: Suppose for some `k >= n, AA j <= k, x^j + (f(x)) in span{1 + (f(x)), ..., x^(n-1) + (f(x))}`

Consider `x^(k+1) + (f(x)) = -a_(n-1)x^(k+1-n+n-1) - ... - a_0x^(k+1-n) + (f(x))`

`= -a_(n-1)x^k - ... - a_0x^(k+1-n) + (f(x))`

`in span{1 + (f(x)), ..., x^(n-1) + (f(x))}` by inductive hypothesis (since `k+1-n <= k`)

`=> x^k + (f(x)) in span{1 + (f(x)), ..., x^(n-1) + (f(x))}`

Any element of `(ZZ // pZZ [x]) / (f(x))` can be written as `sum_(i = 0)^(n-1) b_ix^i + (f(x))`

Therefore, `| (ZZ // pZZ[x]) / (f(x)) | <= p^n`

There are no `ZZ // pZZ` relations among `{1 + (f(x)), ..., x^(n-1) + (f(x))}`

Suppose `sum_(i = 0)^(n-1) c_ix^i + (f(x)) = 0 + (f(x))`

`=> sum_(i = 0)^(n-1)c_ix^i in (f(x)) => f(x)|sum_(i = 0)^(n-1) c_ix^i`

But `deg(f(x)) > n-1`, so that is a contradiction

`{1 + (f(x)), ..., x^(n-1) + (f(x))}` form a basis for `(ZZ // pZZ [x]) / (f(x))` as a vector space over `ZZ // pZZ`

Since the basis has `n` elements, the vector space has cardinality `p^n`

Theorem: `ZZ[x]` is a `UFD` (Unique Factorization Domain). Let `f(x) in ZZ[x]` which is not a unit and not zero. Then we can always write `f(x) = prod_(i = 1)^n p_i prod_(j = 1)^m q_j (x)` where `p_i` are primes in `ZZ` (not necessarily distinct) This factorization is unique: given `f(x) = prod_(i = 1)^n p_i prod_(j =1)^m q_j (x) = prod_(k = 1)^(n') p'_k prod_(l = 1)^(m') q'_l (x)`, we must have `n = n'`, `m = m'` and possibly after renumbering, `p_i = +- p'_i`, `q_j(x) = +- q'_j(x)`

Existence: Induction on the degree of `f`

If `deg(f) = 0`, this follows straight from the fundamental theorem of arithmetic

We can factor out the content of a nonconstant polynomial `f` and apply the fundamental theorem of arithmetic

Therefore, it suffices to prove the result in the case that `f(x)` is a primitive, non-constant polynomial

Claim: Given a primitive polynomial of `deg > 0`, we can write the polynomial as a product of irreducible polynomials

Let `n = deg(f)`

Base Case: n = 1. In this case, `f` is a monic linear polynomial, which is automatically irreducible

Inductive Hypothesis: Suppose that, for some `n >= 1`, `AA k <= n`, for any primitive polynomial `f(x) in ZZ[x]` of degree `k`, `f(x)` can be factored into a product of irreducible polynomials

Suppose `f(x) in ZZ[x]` has degree `n+1` and is primitive

If `f(x)` is irreducible, we are done

Suppose `f(x)` is reducible `=> f(x) = g(x)h(x)` for some `g(x), h(x) in ZZ[x]` `s.t.` `g(x), h(x)` are primitive and neither is a unit

Thus, `deg(g(x)), deg(h(x)) < n + 1`

The inductive hypothesis applies to show that `g(x), h(x)` can be written as products of irreducible polynomials in `ZZ[x]`

Uniqueness: Suppose that `f(x) = prod_(i = 1)^n p_i prod_(j = 1)^m q_j(x) = prod_(k = 1)^(n') p'_k prod_(l = 1)^(m') q'_l(x)`

Since `q_i(x), q'_l(x)` are irreducible, `q_j(x), q'_l(x)` must be primitive

`=>` By Gauss's Lemma, `prod_(j = 1)^m q_j(x)`, `prod_(l = 1)^(m') q'_l(x)` are primitive

Taking the content of both sides, we see that `prod_(i = 1)^n p_i = +- prod_(k = 1)^(n') p'_k`

The uniqueness statement for the `p_i`'s, `p_k`'s follows from the fundamental theorem of arithmetic

Therefore, it suffices to show that given `prod_(j = 1)^m q_j(x) = prod_(l = 1)^(m') q'_l(x)`, then `m = m'`, `q_j(x), q'_l(x)` are irreducible, `q_j(x) = +- q'_l(x)` after reordering

We prove the result by induction on `j`

Base Case: `j = 1`. Since `q_j(x)` is irreducible in `ZZ[x]`, it is irreducible in `QQ[x]` `AA j` (and similarly for all `q'_l(x)`)

From the equation `prod_(j = 1)^m q_j(x) = prod_(l = 1)^(m') q'_l(x)`, we see that `q_1(x) | prod_(l = 1)^(m') q'_l(x) in QQ[x]`

Therefore, `q_1(x) | q'_l(x) in QQ[x]` for some `l => q'_l(x) = q_1(x)h(x)`

Since `q'_l(x)` is irreducible `=> h(x) in QQ[x] \\ {0}`

`q'_l(x) = q_1(x) * a/b => bq'_l(x) = aq_1(x)`

Since `q'_l(x), q_1(x)` are primitive, `a = +- b => a/b = +- 1`

Relabel `q'_l(x) = q'_1(x)`

Inductive Hypothesis: Suppose for some `j AA i <= j`, `q_i(x) = +- q_i(x)` (after reordering)

Given this, we can cancel the common terms on both sides

`prod_(k = 1)^m q_k(x) = prod_(l = 1)^(m') q'_l(x)`

This yields `prod_(k = j + 1)^m q_k(x) = prod_(l = j + 1)^(m') q'_l(x)`

To show that `q_(j+1)(x) = q'_l(x)` for some `j+1 <= l <= m`, we use the same argument as in the base case

We claim `m = m'`

If `m > m', prod_(j = m' + 1)^m q_j(x) = +- 1`, which is a contradiction

If `m < m'`, `prod_(l = m + 1)^(m') q'_l(x) = +- 1`, which is a contradiction

Return to Integral Domains

• Definition: Let `a` and `b` be elements of an integral domain `R`. Then `a` and `b` are associates if `a = br` where `r` is a unit in `R`

• Ex: `x^2 + 1` and `x^2/3 + 1/3` are associates in `QQ[x]`

• Let `a` be an element of an integral domain `R`. `a` is irreducible if whenever `b in R` `s.t.` `b|a`, `a` and `b` are associates

• Definition: Let `p` be an element of an integral domain `R`. `p` is prime if whenever `a, b in R` `s.t.` `p|ab => p|a` or `p|b`

Proposition: Let `R` be an integral domain. Let `p in R` be prime. Then `p` is irreducible

Let `p in R` be prime. Suppose `p = ab` for some `a, b in R`

Then `p|ab`, so since `p` is prime, `p|a` or `p|b`

`p|a => EE r_1 in R` `s.t.` `pr_1 = a`

Substituting, we find `p = ab = pr_1b => r_1b = 1` (since `R` is a domain) `=> b in R^x`

`p|b => EE r_2 in R` `s.t.` `pr_2 = b`

`p = ab = apr_2 => ar_2 = 1` (since R is a domain) `=> a in R^x`

`=> p` is irreducible by definition

• The rings which demonstrate that irreducible elements need not be prime are `ZZ[sqrt d]` where `d != 1` and `d` is not divisible by the square of a prime

• `ZZ[sqrt d] = {a + b sqrt d | a, b in ZZ}`

• Define a function `N: ZZ[sqrt d] -> ZZ^(>= 0)` (called the norm) by `a + b sqrt d |-> |a^2 - b^2d |`

We claim that `N(a + b sqrt d) = 0 <=> a, b = 0`

`(lArr)` obvious

`(=>)` Suppose `a + b sqrt d in ZZ[sqrt d] \\ {0}` such that `N(a + b sqrt d) = 0 <=> | a^2 - b^2d | = 0`

`gcd(a, b)^2 | (a/gcd(a,b))^2 - (b/gcd(a,b))^2d | = 0`

It suffices to prove this in the case that `a` and `b` are coprime

If `d = -1`, then `a^2 + b^2 = 0 <=> a = b = 0`

Suppose `d != -1`. Then some prime `p` must divide `d`

Suppose `a, b` are coprime `s.t.` `a^2-db^2 = 0 => a^2db^2`

`p|d => EE k in ZZ \\ {0}` `s.t.` `pk = d`

`a^2 = pkb^2 => p|a^2`

Since `p` is prime, `p|a => EE n in ZZ` `s.t.` `pn = a`

`a^2 = p^2n^2 = pkb^2`

We can cancel the `p`'s `=> pn^2 = kb^2`

Since `gcd(a,b) = 1`, `p|a => p cancel(|) b <=> p cancel(|) b^2`

Therefore, `p|k => EE m in ZZ \\ {0} k = mp`

But then `d = pk = mpp = p^2m => p^2|d` where `p` is prime, which is a contradiction

• `N(a + b sqrt d)*N(c + e sqrt d) = N((a + b sqrt d)*(c + e sqrt d))`

We claim that `x in ZZ[sqrt d]` is a unit `<=> N(x) = 1`

`(=>)` Suppose `x in ZZ[sqrt d]` is a unit

`=> EE y in ZZ[sqrt d]` `s.t.` `xy = 1`

`N(xy) = N(1) = 1`

`N(xy) = N(x)N(y) = 1`

Since `N(x) in ZZ^(>= 0) => N(x) = 1`

`(lArr)` Suppose `a + b sqrt d = x in ZZ[sqrt d]` is `s.t.` `N(x) = |a^2 - b^2d| = 1`

`|a^2 - b^2d| = |(a + b sqrt d)(a - b sqrt d)| = 1`

`=> (a + b sqrt d)(a - b sqrt d) = 1` or `(a + b sqrt d)(a - b sqrt d) = -1`

`=> a + b sqrt d` is a unit

We claim that if `N(x)` is prime, then `x` is irreducible

Suppose `x = ab`. Then `N(x) = N(a)N(b)`

Since `N(x)` is prime and `N(a), N(b) in ZZ^(>= 0)`, either `N(a) = N(x), N(b) = 1` or `N(a) = 1, N(b) = N(x)`

From the previous proof, either `N(a) = 1` or `N(b) = 1 => a` or `b` is a unit `=> x` is irreducible

• Norm: `N: ZZ[sqrt d] -> ZZ^(>= 0)`, `a + b sqrt d |-> | a^2 - db^2 |` where `d` is not `1` and `d` is divisible by the square of any prime number

• 1) `N(x) = 0 <=> x = 0`

• 2) `N(xy) = N(x)N(y)` `AA x, y in ZZ[sqrt d]`

• 3) `N(x) = 1 <=> x` is a unit in `Z[sqrt d]`

• 4) `N(x)` is prime `=> x` is irreducible

Ex: `ZZ[sqrt 5]` We claim that `2` is irreducible but `2` is not prime

`2 = (a + b sqrt 5)(c + d sqrt 5) => N(2) = N(a + b sqrt 5)N(c + d sqrt 5)`

`=> 4 = | a^2 - 5b^2 | * |c^2 - 5d^2|`

We claim that `cancel(EE)` integers `a,b` `s.t.` `a^2 - 5b^2 = 2`

`=> a^2 = 2 (mod 5)`

`a = 0, 1, 2, 3, 4 (mod 5) => a^2 = 0, 1, 4, 4, 1 (mod 5)`

`cancel(EE) a in ZZ` `s.t.` `a^2 = 2 (mod 5)`

`=> cancel(EE) a, b in ZZ` `s.t.` `a^2 - 5b^2 =2`

We also see that `cancel(EE) a, b in ZZ` `s.t.` `5b^2 - a^2 = 2`

Therefore if `|a^2 - 5b^2|*|c^2 - 5d^2| = 4`, either `|a^2-5b^2| = 4, |c^2-5d^2| = 1` or `|a^2-5b^2| = 1, |c^2-5d^2| = 4`

In either case, `a + b sqrt 5` or `c + d sqrt 5` is a unit of `ZZ[sqrt 5] => 2` is irreducible

We claim that `2` is not prime

`2|4`, yet `4 = (-1-sqrt 5)(1 - sqrt 5)` but `2 cancel(|) (-1-sqrt 5)` and `2 cancel(|) (1 - sqrt 5)`

• In an arbitrary integral domain, irreducible does not imply prime

Proposition: If `R` is a `PID`, then `x in R` is irreducible `=> p` is prime

Let `a, b in R` `s.t.` `x|ab` and `x` is irreducible

Since `x|ab`, `EE y in R` `s.t.` `xy = ab`

Since `x|ab, ab in (x)`

Suppose `x cancel(|) a`. We claim `x|b`

We claim `(x,a) = (1)`

Since `R` is a `PID`, `(x,a) = (z)` for some `z != 0 in R`

`x in (z)` and `a in (z) => z|x` and `z|a`

Since `x` is irreducible and `x cancel(|) a => z` is a unit

Since `(x,a) = (1), EE r_1, r_2 in R` `s.t.` `r_1x + r_2a = 1`

Multiply both sides by `b => r_1xb + r_2ab = b`

`=> r_1xb + r_2xy = b` (since `xy = ab`)

`=> x(r_1b + r_2y) = b => x|b`

Ex: `ZZ[x]` is not a `PID`

Consider `(3,x) sube ZZ[x]`. We claim that this is not a principal ideal

Suppose for contradiction `(3,x) = (f(x))`

Then `f(x)|3` and `f(x)|x => f(x) = +- 1`

Suppose `(3,x) = (1)`

Then `EE g(x), h(x) in ZZ[x]` `s.t.` `3g(x) + xh(x) = 1`

Consider `ev_0: ZZ[x] -> ZZ, q(x) |-> q(0)`

Then `ev_0(1) = 1, ev_0(3g(x) + xh(x)) = 3*g(0) + 0*h(0)`

`= 3*g(0) = 1 => 3|1 in ZZ`, a contradiction

• Definition: Let `R` be an integral domain. Then `R` is a unique factorization domain if every nonzero, non-unit element of `R` can be written as a product of irreducible elements. This factorization is unique up to units

Lemma: In a `PID`, every ascending chain of ideals `I_1 sube I_2 sube ... sube I_n sube ...` must stabilize: `EE m in ZZ^+` `s.t.` `AA m' >= m, I_m = I_(m')`

Let `R` be a `PID`. Let `I_1 sube, ..., sube I_n sube ...` be an ascending chain of ideals.

We claim that `cc I = uuu_(n = 1)^oo I_n` is an ideal

Let `x, y in cc I => EE` indices `n, m` `s.t.` `x in I_n, y in I_m`

Let `n' = max{n, m}`. Then `x,y in I_(n')`

Since `I_(n')` is an ideal, `x + y in I_(n') => x + y in cc I`

Let `z in cc I, r in R`. Then `EE` an index `k` `s.t.` `z in I_k`

Since `I_k` is an ideal, `rz in I_k => rz in cc I`

Therefore, `cc I` is an ideal

Since `R` is a `PID, cc I = (x)` for some `x in R`

Since `(x) = uuu_(n= 1)^oo I_i, x in I_i` for some `i`

Let `n` be the least integer `s.t.` `x in I_n`

Then `(x) = cc I supe I_n`

Since `x in cc I` and `x in I_n => (x) sube I_n => cc I = I_n`

The chain stabilizes after `I_n`

Theorem: If `R` is a `PID`, then `R` is a `UFD`

(Existence) Let `x in R`, not a unit, nonzero. If `x` is irreducible, then `x = x` is the factorization

Suppose `x` is not irreducible. Then we can write `x = x_1y_1` where `x_1y_1 notin R^x`

If `x_1` is irreducible, then at least `1` irreducible element divides `x`

Suppose `x_1` is not irreducible, repeat the process `x_1|x, x_2|x_1, x_3|x_2, ...`

If this process never terminates, we get an ascending chain `(x) sube (x_1) sube (x_2) sube ...`

Since `R` is a `PID`, this chain must stabilize, so the process must terminate

By definition, `EE n in ZZ^+` `s.t.` `x_n = x_(n+1) => x_n | x_(n+1) => EE z in R` `s.t.` `x_nz = x_(n+1)`

Since `x_(n+1)|x_n => EE w in R` `s.t.` `x_(n+1)w = x_n`

Putting the two together, we see that `x_(n+1) = x_nz = x_(n+1)wz`

Since `x_(n+1) != 0` and `R` is a domain `=> wz = 1 => w in R^x`

Therefore, `x_n` is irreducible

We've established the existence of at least `1` irreducible factor of `x`

Thus, every nonzero, non-unit element has at least `1` irreducible factor

Let `x in R` be nonzero and not a unit. Then `EE q_1 in R` irreducible `s.t.` `x = q_1w_1`

If `w_1` is irreducible, then we're done

If not, then `w_1 = q_2w_2`

By the same argument from before, the process cannot continue indefinitely

`w_n = q_(n+1)w_(n+1)` where `w_(n+1)` or `q_(n+1)` is a unit

`x = (prod_(i = 1)^n q_i)w_n` is a product of irreducibles

(Uniqueness) We claim that the factorization of an element into a product of irreducibles is unique up to associates and reordering

Suppose `x = prod_(i = 1)^r p_i = prod_(j = 1)^s q_j`

We claim `p_i = u_iq_i` for some unit `u_i in R` after reordering for each `1 <= i <= r`

Base Case: `i = 1`. `p_1 = prod_(j = 1)^s q_j`

Since `p_1` is irreducible, `R` is a `PID => p_1` is prime

So `p_1|q_j` for some `j`. Relabel this as `q_1`

`p_1|q_1` and `q_1` is irreducible `=> p_1` is an associate of `q_1`

Since `p_1` is not a unit `=> EE v_1 in R^x` `s.t.` `p_1 = q_1v_1`

Set `v_1^-1 = u_1`, then `p_1u_1 = q_1`

Inductive Hypothesis: Suppose for some `j >= 1` `AA 1 <= i <= j` `EE u_i in R^x` `s.t.` `p_iu_i = q_i`

Now we can cancel out the common terms in `prod_(i = 1)^j p_i prod_(k = j+1)^r p_k = prod_(l = 1)^j q_l prod_(n = j+1)^s q_n` to get `prod_(k = j+1)^r p_k = prod_(i = 1)^j u_i prod_(n = j+1)^s q_n`

Repeating the argument from the base case, `EE n'` `s.t.` `p_(j+1)|q_(n')` and `EE u_(j+1) in R^x` `s.t.` `p_(j+1)*u_(j+1) = q_(n')`

Relabel `q_(n') = q_(j+1)`

The same argument from the `F[x]` case proves `r = s`

• Euclidean domains generalize `F[x]` and `ZZ` in that they have a division theorem

• Definition: Let `R` be an integral domain. Then `R` is a Euclidean domain if `EE` a function `d: R\\{0} -> ZZ^(>= 0)` `s.t.`

• 1) `d(a) <= d(ab)` `AA a, b in R\\{0}`

• 2) If `a, b in R` with `b != 0`, then `EE q, r in R` `s.t.` `a = bq + r` with `r = 0` or `d(r) < d(b)`

• Ex: `F[x]` and `ZZ` are Euclidean domains

`ZZ[i]` is a Euclidean domain with `d(a + bi) = a^2 + b^2`

1) Let `a + bi, c + fi in ZZ[i] \\ {0}`

`d(a + bi) = a^2 + b^2`

`d((a + bi)(c + fi)) = ||(a + bi)(c + fi)||^2 = ||a + bi||^2||c + fi||^2 = (a^2 + b^2)(c^2 + f^2)`

`a^2 + b^2 <= (a^2 + b^2)(c^2 + f^2)` since `c^2 + f^2 > 1`

So `d(a + bi) <= d((a + bi)(c + fi))`

2) Let `a + bi, c + fi in ZZ[i]` `s.t.` `c + fi != 0`

Want `q_1, q_2i, r_1, r_2i` `s.t.` `a + bi = (c + fi)(q_1 + q_2i) + (r_1 + r_2i)` where `d(r_1 + r_2i) < d(c + fi) => r_1^2 + r_2^2 < c^2 + f^2`

Notice that `(a + bi)/(c + fi) = (a + bi)/(c^2 + f)*(c - fi) = (ac + bf)/(c^2 + f^2) + (bc - af)/(c^2 + f^2)*i in CC`

Let `q_1` be the closest integer to `(ac + bf)/(c^2 + f^2)`. Let `q_2` be the closest integer to `(bc - af)/(c^2 + f^2)`

`|q_1 - (ac + bf)/(c^2 + f^2)| <= 1/2, |q_2 - (bc - af)/(c^2 + f^2)| <= 1/2`

We've defined `q_1, q_2`

Let `r_1 + r_2i = a + bi - (c + fi)(q_1 + q_2i)`

We claim that `r_1 + r_2i` is `s.t.` `||r_1 + r_2i||^2 < ||c + fi||^2`

`||r_1^2 + r_2i||^2 = ||a + bi - (c + fi)(q_1 + q_2i)||^2`

`= ||c^2 + fi||^2*||(a + bi)/(c + fi) - (q_1 + q_2i)||^2`

`= ||c + fi||^2*||((ac + bf)/(c^2 + f^2) - q_1) + ((bc - af)/(c^2 + f^2) - q_2)i||^2`

`||c + fi||^2*((ac + bf)/(c^2 + f^2) - q_1)^2 + ((bc - af)/(c^2 + f^2) - q_2)^2 <= 1/4||c + fi||^2 + 1/4||c + fi||^2 < ||c + fi||^2`

Theorem: Let `R` be a Euclidean domain. Then `R` is a `PID`

Let `I != (0)` be an ideal of `R`. Let `x in I` `s.t.` `d(x)` is minimal. Such an `x` exists by the well ordering of the natural numbers

We claim that `x` generates `I`, `(x) = I`

`(sube) x in I` and `I` is an ideal `=> (x) sube I`

`(supe)` Let `y in I`. Then `EE q, r in R` `s.t.` `y = xq + r` where `r = 0` or `d(r) < d(x)`

Notice that `r = y - xq`, so `r in I`

Therefore, `d(r)` cannot be less than `d(x)` by minimality of `d(x)`

Thus `r = 0 => x|y => y in (x)`

• `R` is a Euclidean domain `=> R` is a `PID => R` is a `UFD`

Vector Spaces

• Definition: Let `k` be a field. A vector space over `k` is a set `V` equipped with a binary operator `+: V xx V -> V` such that `(V, +)` is an abelian group and another operation `*: k xx V -> V` called scalar multiplication such that

• 1) `a*(x + y) = ax + ay` `AA a in k, x, y in V`

• 2) `(a + b)*x = ax + bx` `AA a, b in k, x in V`

• 3) `a*(bx) = (ab)*x` `AA a, b in k, x in V`

• 4) `1*x = x` `AA x in V, 1 in k`

• Last time we showed that `(ZZ//pZZ [x]) / (f(x))` is a field and a vector space of dimension `= deg(f(x))` if `f(x)` is irreducible over `ZZ // pZZ`

• Definition: Let `V` be a vector space `// k`. A subset `W sube V` is a subspace of `V` if `W` is a `k`-vector space with the operations of `+, *` restricted to `W`

• Proposition: Let `V` be a `k`-vector space and let `W` be a subset of `V`. Then `W` is a subspace of `V` if and only if `cx + dy in W` `AA x, y in W, c, d in k`

• Definition: Let `V` be a vector space `// k`. A set `S sube V` is linearly dependent if `EE v_1, ..., v_n in S` and a linear combination `sum_(i = 1)^n c_iv_i = 0` where at least one `c_i` is nonzero. A set `S sube V` is linearly independent if whenever `v_1, ..., v_m in S` `s.t.` `sum_(i = 1)^m c_iv_i = 0`, we must have `c_i = 0` `AA 1 <= i <= m`

• Definition: Let `V` be a vector space `// k`. Then a set `S sube V` spans `V` if every element of `V` can be written as a `k`-linear combination of elements of `S`. A set `S sube V` is a basis for `V` if `S` spans `V` and `S` is linearly independent

• Definition: A set `S` is called a partially ordered set if `EE` a relation `<=` `s.t.`

• 1) Reflexivity: `a <= a` `AA a in S`

• 2) Anticommutativity: `AA a, b in S` if `a <= b` and `b <= a`, then `a = b`

• 3) Transitivity: If `a <= b` and `b <= c => a <= c` `AA a, b, c in S`

• A chain in a partially ordered set `S` is a subset `cc C sube S` `s.t.` `AA x, y in cc C`, either `x <= y` or `y <= x`. Also known as a totally ordered set or a linearly ordered set. An upper bound for a chain `cc C` in `S` is an element `z in S` `s.t.` `x <= z` `AA x in cc C`

• Zorn's Lemma: Let `S` be a partially ordered set. If every chain in `S` has an upper bound in `S`, then `S` has at least one maximal element

Theorem: Let `V` be a vector space `// k`. Then `V` has a basis

Let `S` be the partially ordered set consisting of all linearly independent subsets of `V`.

If `V = 0`, the result is obvious, so suppose `V != {0}`.

Since `V` is not the zero vector space, then `EE v in V \\ {0}`

By definition, `{v}` is a linearly independent subset of `V` so `S != O/`

Let `cc C = {S_i}_(i in I)` be a chain of elements of `S`. We claim `cc C` has an upper bound in `S`

Let `cc S = uuu_(i in I) S_i`. We claim that `cc S` is linearly independent as well

Suppose `v_1, ..., v_n in cc S` `s.t.` `sum_(j = 1)^n c_(alpha_j)v_(alpha_j) = 0` where `v_(alpha_j) in S_(alpha_j)`

Let `alpha_k = max{alpha_1, ..., alpha_n}`. Then `v_alpha, ..., v_(alpha_n) in S_(alpha_k)`.

Since `S_(alpha_k)` is linearly independent, `c_(alpha_j) = 0` `AA 1 <= j <= n`

Thus `cc S` is linearly independent

Since `S_i sube cc S` `AA i in I`, `cc S` is an upper bound for `cc C`

Since every chain in `S` has an upper bound, `S` has a maximal element, call it `S'`

We claim that `S'` is a basis for `V`

It remains to show that `S'` spans `V`

Suppose not, then `EE v in V` `s.t.` `v in span(S')`

We claim that this implies `S' uu {v}` is linearly independent

Suppose for a contradiction `S' uu {v}` is linearly dependent `=> EE` a linear combination `sum_(k = 1)^m c_(alpha_k)v_(alpha_k) + cv = 0` where `c != 0, v_(alpha_k) in S'`

`V = sum_(k = 1)^m c^-1(-c_(alpha_k))v_(alpha_k) => v in span(S')`, which is a contradiction

Thus, `S' uu {v}` is linearly independent, but this contradicts the fact that `S'` is a maximal linearly independent subset of `V`

Therefore, `cancel(EE) v in V \\ span(S') => span(S') = V`

Proposition: Let `V` be a vector space `// k` that is spanned by a set `G` consisting of exactly `n` vectors and let `L` be a linearly independent subset of `V` containing exactly `m` vectors. Then `m <= n` and `EE` a subset `H sube G` containing exactly `n-m` vectors `s.t.` `L uu H` generates `V`

Base Case: `m = 0`. `|L| = 0 => L != O/`. Take `H = G`

Inductive Hypothesis: Suppose for some `m >= 0`, given any linearly independent subset `L sube V` of cardinality `m`, we must have `m <= n` and `EE H sube G` `s.t.` `|H| = n - m, H uu L` is a spanning set

Let `L` be a linearly independent subset of `V` `s.t.` `|L| = m + 1`

`L = {l_1, ..., l_m, l_(m+1)}`. Consider `L\\{l_(m+1)}`

This is a linearly independent set of cardinality `m`, so the inductive hypothesis applies to show that `m <= n` and `EE H_0 sube G` `s.t.` `|H_0| = n - m` and `H_0 uu L\\{l_(m+1)}` spans `V`

`H_0 = {z_1, ..., z_(n-m)}`

`l_(m+1) in span(H_0 uu L\\{l_(m+1)})`

`l_(m+1) = sum_(i = 1)^(n-m) c_i z_i + sum_(j = 1)^m d_j l_j`

Since `L` is linearly independent, we cannot have `c_1 = ... = c_(n-m) = 0`. Therefore, at least one `c_i` must be nonzero, say `c_k != 0`

Notice `l_(m+1) = sum_(i = 1)^(k-1) c_i z_i + c_k z_k + sum_(h = k + 1)^(n-m) c_h z_h + sum_(j = 1)^m d_j l_j`

`-c_k z_k = sum_(i = 1)^(k-1) c_i z_i + sum_(h = k+1)^(n-m) c_h z_h + sum_(j = 1)^m d_j l_j - l_(m+1)`

`z_k = sum_(i = 1)^(k-1) (-c_k)^-1 c_i z_i + sum_(h = k + 1)^(n+m) (-c_k)^-1 c_h z_k + sum_(j = 1)^m (-c_k)^-1 d_j l_j + (c_k)^-1 l_(m+1)`

`z_k in span(H_0\\{z_k} uu L)`

`{z_1, ..., z_(n-m)} uu {l_1, ..., l_m}` spans `V`

We claim `{z_1, ..., z_(k-1), z_(k+1), ..., z_(n-m)} uu {l_1, ..., l_(m+1)}` spans `V`

Since `z_k in span({z_1, ..., z_(k-1), z_(k+1), ..., z_(n-m)} uu {l_1, ..., l_(m+1)})`

`=> span({z_1, ..., z_(k-1), z_(k+1), ..., z_(n-m)} uu {l_1, ..., l_(m+1)})` `>= span({z_1, ..., z_(k-1), z_k, z_(k+1), ..., z_(n-m)} uu {l_1, ..., l_(m+1)}) = V`

We proved that `(L uu H_0\\{z_k})` spans `V`

This set has cardinality `n` and the cardinality of `L` is `m + 1 => m + 1 <= n`

• Suppose `beta_1, beta_2` are finite bases for `V`

• Let `G = beta_1, L = beta_2`. Then `|beta_2| <= |beta_1|`

• Let `G = beta_2, L = beta_1`. Then `|beta_1| <= |beta_2|`

• Thus, any two finite bases for `V` have the same cardinality

• The dimension of a vector space is the cardinality of a basis

Extension Fields

• We've seen that if `k` is a field and `f(x)` is a polynomial in `k[x]` which is irreducible over `k`, then `k[x] // (f(x))` is a field

• `k[x] // (f(x))` has a subfield isomorphic to `k: {a + (f(x)) | a in k}`

• Definition: Let `k` be a field. A field `L` is an extension field of `k` if `EE` an injective ring homomorphism `f: k -> L`. `L // k` is a field extension

• `L // k` does not mean we are taking a quotient

• Definition: Let `phi_1: k -> L`, `phi_2: k -> L'` be field extensions of `k`. An isomorphism of field extensions is an isomorphism of fields `psi: L -> L'` `s.t.` `psi @ phi_1 = phi_2 <=> bar phi_2 @ psi|_(Im(phi_1)) @ bar phi_1 = i``d_k`



Theorem: Let `k` be a field. Let `f(x) in k[x]` be irreducible over `k`. Then there exists a field extension `L // k` `s.t.` `f(x)` has a root in `L`

We've seen that `k(x) // (f(x))` is a field when `f(x) in k[x]` is irreducible over `k`

We've also seen that `k[x] // (f(x))` contains a subfield which is isomorphic to `k`

By definition, `k[x] // (f(x))` is an extension field of `k`

Let `f(x) = sum_(i = 0)^n a_ix^i`. We claim that `f` has a root in `k[x] // (f(x))`

We claim that `f(t) in (k[x])/(f(x)) [t]` has a root in `k[x]//(f(x))`

`f(t) = sum_(i = 0)^n (a_i + (f(x))) t^i`

Observe that `f(x + (f(x))) = sum_(i = 0)^n (a_i + (f(x)))(x + (f(x)))^i`

`= sum_(i = 0)^n (a_i + (f(x)))(x^i + (f(x))) = sum_(i = 0)^n (a_ix^i + (f(x)))`

`= sum_(i = 0)^n a_ix^i + (f(x)) = 0 + (f(x))`

Therefore `L` is an extension field of `k` which has a root of `f`

• Kronecker's Theorem: Let `f(x) in k[x]` be a nonconstant polynomial. Then there exists a field extension `L // k` `s.t.` `f(x)` has at least one root in `L`

• Definition: Let `k sube L` be fields. Let `z_1, ..., z_n in L`. Then `k(z_1, ..., z_n)` is the smallest field contained in `L` containing `z_1, ..., z_n` and `k`

Ex: Consider `x^3 - 2 in QQ[x]`. By Eisenstein's Criterion, `x^3 - 2` is irreducible over `QQ`

Therefore, `x^3-2` has no roots in `QQ`. Consider `QQ(root(3)(2))`

`QQ(root(3)(2)) = {a + b root(3)(2) + c root(3)(4) | a,b,c in QQ}`. This does not contain all the roots of `x^3-2`

The roots of `x^3 - 2` are `root(3)(2), (e^(i*(2pi)/3))(root(3)(2)), (e^(i*(4pi)/3))(root(3)(2))`

`QQ(e^(i*(2pi)/3), root(3)(2)) = {a_1 + a_2 root(3)(2) + a_3 e^(i*(2pi)/3) + a_4 e^(i*(2pi)/3) root(3)(2) + a_5 root(3)(4) + a_6 e^(i*(2pi)/3) root(3)(4) | a_1, ..., a_6 in QQ}`

`e^(i*(4pi)/3), e^(i*(4pi)/3) root(3)(2), e^(i*(4pi)/3) root(3)(4), e^(i*(2pi)/3), 1, e^(i*(4pi)/3)` are the roots of `x^3 - 1`

`QQ(e^(i*(2pi)/3), root(3)(2))` contains all the roots of `x^3 - 2`

`x^3 - 1 = (x-1)(x-e^(i*(2pi)/3))(x-e^(i*(4pi)/3))`

Notice that the coefficient on `x^2` on both sides have to be equal

`=> 0 = -1-e^(i*(2pi)/3) - e^(i*(4pi)/3) => e^(i*(4pi)/3) = -1-e^(i*(2pi)/3)`

• Definition: Let `k` be a field. Let `f(x) in k[x]`. Let `L // k` be a field extension. We say that `f(x)` splits in `L` if (the image of) `f(x)` factors into a product of linear terms in `L[x]`. `L` is called a splitting field for `f(x)` if `L` is equal to the subfield of `L` generated by the image of `k` and the roots `alpha_1, ..., alpha_n in L => L = phi(k)(alpha_1, ..., alpha_n)`. `phi: k -> L`. `L ~= k(alpha_1, ..., alpha_n)`

We claim that `QQ(root(3)(2), e^(i*(2pi)/3))` is a splitting field for `x^3 - 2`

Certainly `x^3 - 2` splits in `QQ(root(3)(2), e^(i*(2pi)/3))`

We've already seen that it is necesasary and sufficient to contain the first two roots

If `L` is a field containing the first two roots, `root(3)(2)` and `e^(i*(2pi)/3) root(3)(2)`, then `(e^(i*(2pi)/3) root(3)(2))/root(3)(2) = e^(i*(2pi)/3) in L`

This implies `QQ(root(3)(2), e^(i*(2pi)/3)) sube L`

Notice that `QQ(root(3)(2)) sube RR`, so this cannot be a splitting field

Also, `QQ(e^(i*(2pi)/3))` is not a splitting field

`a + be^(i*(2pi)/3) = root(3)(2)`

If this were the case, taking real and imaginary parts, we see that `b = 0 => a = root(3)(2) in QQ`, which is a contradiction

A splitting field must contain `QQ(root(3)(2)), QQ(e^(i*(2pi)/3)) =>` it must contain `QQ(root(3)(2), e^(i*(2pi)/3)) => QQ(root(3)(2), e^(i*(2pi)/3))` is a splitting field

Theorem: Let `f(x) in k[x]` be a nonconstant polynomial. Then there exists a splitting field for `f(x)`

We prove the result by induction on `deg(f(x))`

Base Case: `deg(f(x)) = 1`. Then `f(x)` has a single root and the root lies in `k`.

Thus, `k` itself is a splitting field for `f(x)` over `k`

Inductive Hypothesis: Suppose that for all fields `k`, for some integer `n >= 1`, for all polynomials `g(x)` `s.t.` `deg(g(x)) = n`, there exists a splitting field for `g(x)` over `k`

Let `f(x)` be a polynomial of degree `n+1` in `k[x]`

Notice that `f(x)` has a root in `k[x] // (f(x)) = L` by Kronecker's Theorem

Therefore, in `L[t]`, we can use the Division Theorem to write `f(t) = (t - (x + (f(x))))q(t)`

Notice that `deg(q(t)) = n`, so by the inductive hypothesis, there exists a splitting field for `q(t)` over `L, L'`

From the definition, `L'` is a splitting field for `f(x)` over `k`

Let `f(x) in k[x]`. Suppose that `f` is irreducible over `k` and has a root in some field extension `L // k`, call the root `alpha in L`. Then there exists an isomorphism `k[x] // (f(x)) ~= phi(k)(alpha)` where `phi: k -> L` is injective

We define `psi: k[x] -> phi(k)(alpha), g(x) |-> phi(g)(alpha)`. `psi` is surjective

We claim that `ker(psi) = (f(x))`

`(supe)` Notice that if `q(x) in (f(x))`, then `q(x) = h(x)f(x)` for some `h(x) in k[x]`

`psi(q(x)) = psi(h(x))psi(f(x)) = phi(h)(alpha)phi(f)(alpha) = 0 => q(x) in ker(psi)`

Method 1: Notice that there is a well-defined ring homomorphism `bar psi: k[x] // (f(x)) -> phi(k)(alpha), g(x) + (f(x)) |-> phi(g)(x) = psi(g(x))`

This is well-defined since `(f(x)) in ker(psi)`. `bar psi` is surjective since `psi` is surjective

Notice that since `bar psi` is not the zero map, it must be injective, for `ker(bar psi)` is either `0` or `k[x] // (f(x))` and it is not the latter

Therefore `bar psi` is an isomorphism

If `gamma: F -> G` is a map of fields, it is either the zero map or it is injective

Method 2: `(sube)` Let `g(x) in ker(psi)`. We claim that `g(x) in (f(x))`

It suffices to show that `(g(x), f(x)) = (f(x))`

Since `k` is a field, `k[x]` is a `PID` `=> (g(x), f(x)) = (h(x))` for some `h(x) in k[x]`

This implies that `g(x), f(x)` are divisible by `h(x)`

Suppose for a contradiction `f(x) cancel(|) g(x)`

Since `f(x)` is irreducible, `h(x)` must be an associate of `f(x)`, or `h(x)` must be a unit in `k[x]`

Since `h(x)|g(x)`, then `h(x)` cannot be an associate of `f(x)`, otherwise `h(x)|g(x) => f(x)|g(x)`, which is a contradiction

Thus, `h(x) in k^x`. Therefore `(g(x), f(x)) = (1)`

Then `EE q_1(x), q_2(x) in k[x]` `s.t.` `g(x)q_1(x) + f(x)q_2(x) = 1`

`psi(g(x)q_1(x) + f(x)q_2(x)) = psi(1)`

`=> 0*psi(q_1(x)) + 0*psi(q_2(x)) = 1 => 0 = 1`, which is a contradiction

Therefore, `(g(x), f(x)) = (f(x)) => f(x)|g(x) => g(x) in (f(x))`

• In general, we see that given `phi: k -> L`, `alpha in L` a root of `f(x)` where `f(x)` is irreducible, `EE` an isomorphism `k[x]//(f(x)) ~= phi(k)(alpha)`

Proposition: Let `f(x) in k[x]` be nonconstant. Let `phi: k -> k'` be an isomorphism of fields. Let `L, L'` be splitting fields for `f(x)`, `phi(f(x))` over `k, k'` respectively. Let `alpha in L` be a root of `f(x)`, `beta in L'` be a root of `phi(f(x))`. Let `phi_1: k -> L, phi_2: k' -> L'` be injective ring homomorphisms exhibiting `L, L'` as extensions of `k, k'` respectively. Then `EE` an isomorphism `psi: phi_1(k)(alpha) ~= phi_2(k')(beta)` `s.t.` `psi|_(phi_1(k)) @ phi_1 = phi_2 @ phi`

Notice that since `phi: k -> k'` is an isomorphism, there is an induced isomorphism `phi[x]: k[x] -> k'[x]`

Since `phi[x]` is an isomorphism, `phi[x]^-1((phi(f(x)))) = (f(x))`

Thus, there is an isomorphism `k[x] // (f(x)) ~= k[x] // (phi(f(x)))`

Since `alpha, beta` are roots of `f(x)`, `phi(f(x))` in `L, L'` respectively, the previous result shows that `k[x] // (f(x)) ~= phi_1(k)(alpha)`, `k[x] // (phi(f(x))) ~= phi_2(k')(beta)`

Let `f(x)` be a nonconstant polynomial in `k[x]`. Then any two splitting fields for `f(x)` are isomorphic

Let `phi_1: k -> L`, `phi_2: k' -> L'` be the injective ring homomorphisms exhibiting `L // k`, `L' // k'` as field extensions

Let `H = phi_1(k)`, `H' = phi_2(k')`

Base Case: Suppose `f(x)` has degree `1`. Then `f(x)` has a single root `alpha in k`, so `f(x) = cx + d, c,d in k`

Then `0 = phi_1(0) = phi_1(f(alpha)) = phi_1(c)phi_1(alpha) + phi_1(d)` and `0 = phi_2(0) = phi_2(f(alpha)) = phi_2(c)phi_2(alpha) + phi_2(d)`

Thus, `phi_1(alpha), phi_2(alpha)` are roots of `phi_1(f), phi_2(f)` respectively

Since `phi_1(alpha) in H, phi_2(alpha) in H'`, we see that `H` and `H'` are splitting fields for `f` over `k` `=> H = L, H = L'`

Notice that `phi_2|_(H') @ (phi_1|_H)^-1: H -> H'` is an isomorphism

Inductive Hypothesis: Suppose for any field `k`, for some integer `n >= 1`, for any polynomial `f(x)` of degree `n`, any two splitting fields for `f(x)` are isomorphic

Suppose that `f(x) in k[x]` has degree `n+1`. Let `L, L'` be splitting fields for `f(x) // k`

Let `f_1(x)` be an irreducible factor of `f(x)`

Since `L, L'` are splitting fields for `f(x)` over `k`, `EE alpha in L, beta in L'` `s.t.` `alpha` is a root of `phi_1(f_1(x))` and `beta` is a root of `phi_2(f_1(x))`

By the previous result, there exists an isomorphism `psi_1: H(alpha) -> H'(beta)` which restricts to `phi_2 @ phi_1^1` on `H`

Since `alpha` is a root of `phi_1(f(x))`, `beta` is a root of `phi_2(f(x))`, we can write `phi_1(f(x)) = (x - alpha)q_1(x) in H(alpha)(x)`, `phi_2(f(x)) = (x - beta)q_2(x) in H'(beta)(x)`

Notice that `psi_1(q_1(x)) = q_2(x)`, `deg(q_1(x)) = n`

`L, L'` are splitting fields for `q_1(x)` over `H(alpha)`

By the inductive hypothesis, `L ~= L'`

• Definition: Let `f(x) in k[x]`. Let `L` be a splitting field for `f` over `k`. Let `alpha` be a root of `f(x)` in L[x]`. `alpha` is a root of multiplicity m if `m` is the multiplicity of `x-alpha` as a factor in the factorization of `f(x)` as a product of linear terms in `L[x]`

• `f(x) = (x-alpha)^m q(x) in L[x]` where `(x - alpha) cancel(|) q(x)`

• Definition: Let `f(x) = sum_(i = 0)^n a_ix^i in k[x]`. The (formal) derivative of `f(x)` is the element `f'(x) = sum_(i = 1)^n ia_ix^(i-1)`

• This satisfies the same properties as it does in calculus

Proposition: Let `f(x) in k[x]`. Then `f(x)` has a root of multiplicity `> 1` if and only if `f(x)` and `f'(x)` have a nonconstant greatest common divisor in `k[x]`

`(=>)` Let `L` be a splitting field for `f(x)` over `k`

Let `alpha` be a root of multiplicity `> 1`, call the multiplicity `m`

By definition, in `L[x]`, `f(x) = (x - alpha)^m q(x)` where `(x - alpha) cancel(|) q(x)`

`f'(x) = m(x-alpha)^(m-1) q(x) + (x - alpha)^m q'(x)`

`f'(alpha) = m(alpha-alpha)^(m-1) q(alpha) + (alpha-alpha)^m q(alpha)`

`= 0*q(alpha) + 0*q'(alpha) = 0`

Thus, `f(x)` and `f'(x)` have a common zero, `alpha`

Suppose for a contradiction that `gcd(f(x), f'(x)) = 1 in k[x]`

This implies that `EE q_1(x), q_2(x) in k[x]` `s.t.` `f(x)q_1(x) + f'(x)q_2(x) = 1` in `k[x]`

This same formula holds in `L[x]`, so `f(x)q_1(x) + f'(x)q_2(x) = 1 in L[x]`

Consider evaluating at `alpha`

`ev_alpha: L[x] -> L`, `g(x) |-> g(alpha)`

`ev_alpha(f(x)q_1(x) + f'(x)q_2(x)) = ev_alpha(1) = 1`

`= f(alpha)q_1(alpha) + f'(alpha)q(alpha) = 1 = 0*q_1(x) + 0*q_2(x) = 0`, which is a contradiction

`(⇐)` Suppose `EE g(x) in k[x]` which is a nonconstant such that `(g(x)) = (f(x), f'(x))`

Let `alpha` be a root of `g(x)` in `L`. Then `x-alpha` divides `g(x)` in `L[x]`, so it divides both `f(x)` and `f'(x)` in `L[x]`

Using the Division Theorem, we can write `f(x) = (x-alpha)q(x)`

Using the properties of the formal derivative, `f'(x) = q(x) + (x-alpha)q'(x)`

Since `alpha` is a root of `f'(x) => f'(alpha) = 0 = q(alpha) + (alpha-alpha)q'(alpha) => q(alpha) = 0 <=> (x-alpha)|q(x)`

Since `(x-alpha)|q(x) => EE q_1(x) in L[x]` `s.t.` `(x-alpha)q_1(x) = q(x)`

Plugging this back in to `f(x)`, we see that `f(x) = (x- alpha)^2q_1(x) => alpha` is a root of multiplicity `>= 2`

Corollary: Let `f(x) in k[x]` be irreducible. If `char(k) = 0`, then `f(x)` cannot have multiple roots. If `char(k) = p`, then `f(x)` has a multiple root in a splitting field `L` if and only if `EE g(x) in k[x]` `s.t.` `f(x) = g(x^p)`